题目内容
在一直角坐标系中，点A、点B的坐标分别为（-4，0）、（0，3），则坐标原点O到线段AB的距离为
- A.2
- B.2.4
- C.5
- D.6
B
分析：在直角坐标系中利用勾股定理求出线段AB的长，然后利用面积相等的方法求得原点到线段AB的距离．
解答：在坐标系中，OA=4，OB=3，
∴由勾股定理得：AB=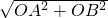
=
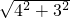=5，
设点O到线段AB的距离为h，
∵S△ABO=
OA•OB=AB•h，
∴3×4=5h，
解得h=2.4．
故选B．
点评：本题考查了勾股定理的知识，利用面积相等求直角三角形的斜边上的高是长采用的方法．
分析：在直角坐标系中利用勾股定理求出线段AB的长，然后利用面积相等的方法求得原点到线段AB的距离．
解答：在坐标系中，OA=4，OB=3，
∴由勾股定理得：AB=
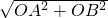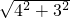==5，设点O到线段AB的距离为h，
∵S△ABO=
OA•OB=AB•h，∴3×4=5h，
解得h=2.4．
故选B．
点评：本题考查了勾股定理的知识，利用面积相等求直角三角形的斜边上的高是长采用的方法．
练习册系列答案
相关题目
暑假期间，王明到承德雾灵山风景区--景区主峰为燕山最高峰（海拔达1834米），位于承德市兴隆县境内旅游．导游介绍山区气温会随着海拔高度的增加而下降，提醒大家上山要多带一件衣服，王明从旅馆中得到一份残缺的雾灵山地区海拔和气温数据表（温差不超过2℃），数据如下：
（1）以海拔高度为x轴，根据上表提供的数据在下列直角坐标系中描点并连线；
（2）观察（1）中所画出的图象，猜想y与x之间函数关系，求出所猜想的函数关系表达式，并根据表中提供的数据验证你的猜想；
（3）如果气温低于20℃就需要穿外套，请问王明需不需要携带外套上山？
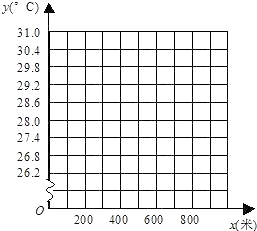
| 海拔高度x（米） | 400 | 500 | 600 | 700 | 800 | … |
| 气温y（℃） | 29.2 | 28.6 | 28.0 | 27.4 | 26.8 | … |
（2）观察（1）中所画出的图象，猜想y与x之间函数关系，求出所猜想的函数关系表达式，并根据表中提供的数据验证你的猜想；
（3）如果气温低于20℃就需要穿外套，请问王明需不需要携带外套上山？
在一直角坐标系中，点A、点B的坐标分别为（-4，0）、（0，3），则坐标原点O到线段AB的距离为（ ）
| A、2 | B、2.4 | C、5 | D、6 |
在平面直角坐标系中，点P从原点O出发，每次向上平移2个单位长度或向右平移1个单位长度．
（1）实验操作：
在平面直角坐标系中描出点P从点O出发，平移1次后，2次后，3次后可能到达的点，并把相应点
的坐标填写在表格中：
（2）观察发现：
任一次平移，点P可能到达的点在我们学过的一种函数的图象上，如：平移1次后在函数 的图象上；平移2次后在函数 的图象上…由此我们知道，平移n次后在函数 的图象上．（请填写相应的解析式）
（3）探索运用：
点P从点O出发经过n次平移后，到达直线y=x上的点Q，且平移的路径长不小于50，不超过56，求点Q的坐标．
（1）实验操作：
在平面直角坐标系中描出点P从点O出发，平移1次后，2次后，3次后可能到达的点，并把相应点
的坐标填写在表格中：| P从点O出发平移次数 | 可能到达的点的坐标 |
| 1次 | （0，2），（1，0） |
| 2次 | |
| 3次 |
任一次平移，点P可能到达的点在我们学过的一种函数的图象上，如：平移1次后在函数
（3）探索运用：
点P从点O出发经过n次平移后，到达直线y=x上的点Q，且平移的路径长不小于50，不超过56，求点Q的坐标．