题目内容
【题目】如图:△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD,DE,BE,则下列结论:①∠ECA=165°,②BE=BC;③AD⊥BE;其中正确的是_________
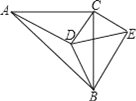
【答案】①②③
【解析】如图,(1)∵AC=AD,∠CAD=30°,
∴∠ACD=∠ADC=![]() ,
,
∵CE⊥DC,∴∠DCE=90°,∴∠ACE=∠ACD+∠DCE=165°.故①正确;
(2)由(1)可知:∠ACB=∠DCE=90°,
∴∠ACE-∠DCB=∠DCE-∠DCB,即∠ACD=∠BCE,
在△ACD和△BCE中, 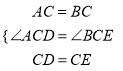 ,
,
∴△ACD≌△BCE,∴BE=AD=BC.故②正确;
(3)延长AD交BE于点F,∵△ACD≌△BCE,∴∠2=∠CAD=30°,
∵AC=BC,∠ACB=90°,∴∠CAB=∠3=45°,∴∠1=∠CAB-∠CAD=15°,
∴∠AFB=180°-∠1-∠2-∠3=90°,∴AD⊥BE.故③正确;
综上所述:正确的结论是①②③.

练习册系列答案
相关题目