题目内容
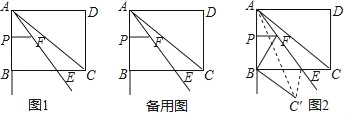
如图1,矩形ABCD中,AB=4,AD=5,E为BC上一点,BE:CE=3:2,连接AE,点P从点A出发,沿射线AB的方向以每秒1个单位长度的速度匀速运动,过点P作PF∥BC交直线AE于点F.
(1)线段AE= ;
(2)设点P的运动时间为t(s),EF的长度为y,求y关于t的函数关系式,并写出t的取值范围;
(3)当t为何值时,以F为圆心的⊙F恰好与直线AB、BC都相切?并求此时⊙F的半径;
(4)如图2,将△AEC沿直线AE翻折,得到△AEC',连结AC',如果∠ABF=∠CBC′,求t值.(直接写出答案,不要求解答过程).
练习册系列答案
相关题目


 ,
,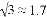 ,
,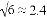 ).
).
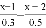 =1.2中的分母化为整数,得
=1.2中的分母化为整数,得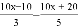 =12;④平面内有4个点,过每两点画直线,可画6条.其中正确的有( )
=12;④平面内有4个点,过每两点画直线,可画6条.其中正确的有( )

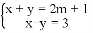 的解满足2x+3y>0,则m满足的亲件是_____.
的解满足2x+3y>0,则m满足的亲件是_____. (k≠0,x<0)的图象过等边△AOB的顶点A.已如点B在x轴上,且B(﹣4,0).
(k≠0,x<0)的图象过等边△AOB的顶点A.已如点B在x轴上,且B(﹣4,0).