题目内容
我们已经学过整式的加减,知道进行整式的加减的关键就是各同类项系数的加减.因此我们可以用竖式计算.
例如,计算(2x3-x2+x)+(-x+x2+1)时,我们可以用下列竖式计算:
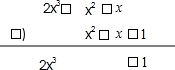
解:∴(2x3-x2+x)+(-x+x2+1)
=2x3+1.
请你仿照上例,计算下列各题.
(1)(a2-2a-2)+(3a-1);
(2)(3a2b-ab2-c)+(ab2+3c- a2b)-(c+2a2b-5ab2).
a2b)-(c+2a2b-5ab2).
解:(1)
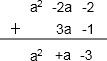
故原式=a2+a-3.
(2)原式可化为:(3a2b-ab2-c)+(- a2b+ab2+3c)+(-2a2b+5ab2-c).
a2b+ab2+3c)+(-2a2b+5ab2-c).
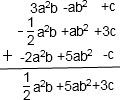
故原式= a2b+5ab2+3c.
a2b+5ab2+3c.
分析:此题实际考查的是合并同类项的运算,观察例题,在列竖式计算中,可将两个多项式中的同类项列在同一竖列中,然后将同类项的系数相加,字母和字母的指数不变;(1)题直接套用上面的方法即可;(2)题中,首先将减法转化为加法,然后再进行计算.
点评:此题的难度并不大,只要熟练掌握去括号以及合并同类项的法则,即可正确的解题.
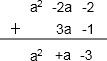
故原式=a2+a-3.
(2)原式可化为:(3a2b-ab2-c)+(-
 a2b+ab2+3c)+(-2a2b+5ab2-c).
a2b+ab2+3c)+(-2a2b+5ab2-c).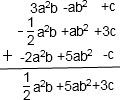
故原式=
 a2b+5ab2+3c.
a2b+5ab2+3c.分析:此题实际考查的是合并同类项的运算,观察例题,在列竖式计算中,可将两个多项式中的同类项列在同一竖列中,然后将同类项的系数相加,字母和字母的指数不变;(1)题直接套用上面的方法即可;(2)题中,首先将减法转化为加法,然后再进行计算.
点评:此题的难度并不大,只要熟练掌握去括号以及合并同类项的法则,即可正确的解题.

练习册系列答案
相关题目
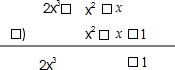
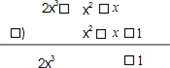
 a2b)﹣(c+2a2b﹣5ab2).
a2b)﹣(c+2a2b﹣5ab2).