题目内容
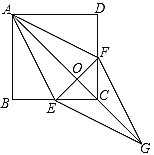
【题目】如图,长方形![]() 在平面直角坐标系中,
在平面直角坐标系中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 为等腰三角形时,
为等腰三角形时,![]() 点的坐标为____________
点的坐标为____________

【答案】![]() ,
,![]() 或
或![]()
【解析】
由题意利用矩形性质和勾股定理求得AD的长,然后分AD=PD=5时,AD=AP=5时,AP=AD时三种情况,设P点坐标为(x,3),结合矩形性质和勾股定理求得P点坐标
解: 由题意可知:AB=OC=8,AO=BC=3
∵D为OC中点
∴OD=CD=4
∴在Rt△AOD中,![]()
当AD=PD=5时,△ADP是等腰三角形
又因为点P在线段AB上,
∴设P点坐标为(x,3),
则![]()
解得:x=0(不合题意,舍去)或x=8
∴此时P(8,3)

当AD=AP=5时,△ADP是等腰三角形
过点P作PE⊥OC,则四边形AOEP是矩形
∴此时P点坐标为(5,3)

当AP=AD时,△ADP是等腰三角形
设 P(x,3),过点P作PE⊥OC,则DE=4-x,AP=AD=x,PE=3
∴在Rt△PED中,![]()
解得:![]()
∴此时P点坐标为(![]() ,3)
,3)

综上所述,点P的坐标为![]() ,
,![]() 或
或![]() .
.
故答案为:![]() ,
,![]() 或
或![]() .
.

练习册系列答案
相关题目