题目内容
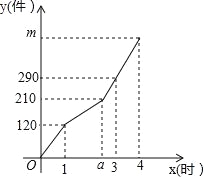
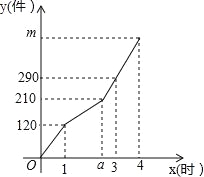
【题目】某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.
(1)甲车间每小时生产产品 件,a= .
(2)求乙车间更换新设备之后y与x之间的函数关系式,并求m的值.
(3)若乙车间在开始更换新设备时,增加两名工作人员,这样可便更换设备时间减少0.5小时,并且更换后工作效率提高到原来的2倍,那么两个车间完成原任务量需几小时?
【答案】(1)60,![]() 小时;
小时;
(2)乙车间更换新设备之后y与x之间的函数关系式为:y=160x﹣190,
∴m=450件;
(3)两个车间完成原任务量需要的时间是![]() 小时.
小时.
【解析】
试题分析:(1)由开始甲、乙两个车间工作效率相同,于是得到开始甲、乙两个车间工作效率是每小时生产产品60个,即可得到结论;
(2)设乙车间更换新设备之后y与x之间的函数关系式为:y=kx+b,把(![]() ,210),(3,290)代入y=kx+b列方程组即可得到结论;
,210),(3,290)代入y=kx+b列方程组即可得到结论;
(3)根据两个车间完成原任务量需要的时间=乙车间更换新设备前的时间+乙车间更换新设备中的时间+乙车间更换新设备后的时间,即可得到结论.
试题解析:(1)∵开始甲、乙两个车间工作效率相同,
∴开始甲、乙两个车间工作效率是每小时生产产品60个,
∴a=![]() +1=
+1=![]() 小时,
小时,
故答案为:60,![]() 小时;
小时;
(2)设乙车间更换新设备之后y与x之间的函数关系式为:y=kx+b,
把(![]() ,210),(3,290)代入y=kx+b得:
,210),(3,290)代入y=kx+b得: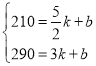 ,
,
∴![]() ,
,
∴乙车间更换新设备之后y与x之间的函数关系式为:y=160x﹣190,
当x=4时,y=450,
∴m=450件;
(3)两个车间完成原任务量需要的时间=乙车间更换新设备前的时间+乙车间更换新设备中的时间+乙车间更换新设备后的时间,
即1+(![]() ﹣1﹣
﹣1﹣![]() )﹣
)﹣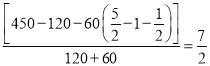
答:两个车间完成原任务量需要的时间是![]() 小时.
小时.

 通城学典默写能手系列答案
通城学典默写能手系列答案