题目内容
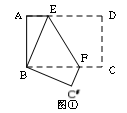
将矩形纸片ABCD分别沿两条不同的直线剪两刀,使剪得的三块纸片恰能拼成一个三角形(不能有重叠和缝隙).图1中提供了一种剪拼成等腰三角形的示意图.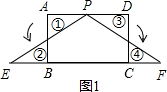
(1)请提供另一种剪拼成等腰三角形方式,并在图2中画出示意图;
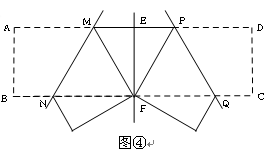
(2)以点B为原点,BC所在的直线为x轴建立平面直角坐标系(如图3),点D的坐标(8,5).若剪拼后得到等腰三角形MNP,使M,N点在y轴上(M在点N上方),点P在边CD上(不与C,D重合).设直线PM的解析式为y=kx+b(k≠0),则k的值为
分析:(1)可直接沿AD,CD中点,BC,CD中点剪开;
(2)△MNP是等腰三角形,分①PM=PN,②PM=MN,③PN=MN三种情况取AD、BC的中点E、F,沿PE、PF剪开,拼接成等腰三角形,然后求出相应的k值与b的取值范围(或b的值),即可得解.
(2)△MNP是等腰三角形,分①PM=PN,②PM=MN,③PN=MN三种情况取AD、BC的中点E、F,沿PE、PF剪开,拼接成等腰三角形,然后求出相应的k值与b的取值范围(或b的值),即可得解.
解答:解:(1)如图所示:
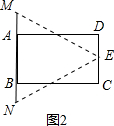
沿AD,CD中点,BC,CD中点剪开,即可得到一个等腰三角形.
(2)
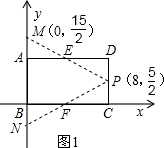
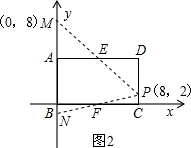
取AD、BC的中点E、F,
①如图1,若PM=PN,把点P(8,
)、M(0,
)代入y=kx+b,求出k=-
,
当PM与AC重合时,b=5,PN与BD重合时,b=10,
所以,5<b<10,
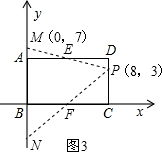
②如图2,若PM=MN,则PM=MN=10,
所以,EP=5,
∵ED=
AD=
×8=4,
∴DP=
=3,
∴CP=5-3=2,
∴点P(8,2),点M(0,8),
代入y=kx+b,求得k=-
,b=8;
③如图3,若PN=MN,则PN=MN=10,
所以,PF=5,
∵FC=
BC=
×8=4,
∴PC=
=3,
∴点P(8,3),点M(0,7),
代入y=kx+b,求得k=-
,b=7;
综上所述,k值为:-
或-
或-
,b的取值范围是5<b<10.
故答案为:-
或-
或-
;5<b<10.

沿AD,CD中点,BC,CD中点剪开,即可得到一个等腰三角形.
(2)



取AD、BC的中点E、F,
①如图1,若PM=PN,把点P(8,
| 5 |
| 2 |
| 15 |
| 2 |
| 5 |
| 8 |
当PM与AC重合时,b=5,PN与BD重合时,b=10,
所以,5<b<10,
②如图2,若PM=MN,则PM=MN=10,
所以,EP=5,
∵ED=
| 1 |
| 2 |
| 1 |
| 2 |
∴DP=
| 52-42 |
∴CP=5-3=2,
∴点P(8,2),点M(0,8),
代入y=kx+b,求得k=-
| 3 |
| 4 |
③如图3,若PN=MN,则PN=MN=10,
所以,PF=5,
∵FC=
| 1 |
| 2 |
| 1 |
| 2 |
∴PC=
| 52-42 |
∴点P(8,3),点M(0,7),
代入y=kx+b,求得k=-
| 1 |
| 2 |
综上所述,k值为:-
| 5 |
| 8 |
| 3 |
| 4 |
| 1 |
| 2 |
故答案为:-
| 5 |
| 8 |
| 3 |
| 4 |
| 1 |
| 2 |
点评:本题主要考查对于一次函数图形的应用以及等腰三角形的性质的掌握,(2)第一种情况b是一个取值范围,第二三两种情况b是一个值.

练习册系列答案
相关题目
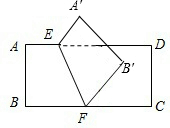 如图,将矩形纸片ABCD沿EF折叠(E、F分别是AD、BC上的点),使点B与四边形CDEF内一点B′重合,若∠B′FC=50°,则∠AEF等于( )
如图,将矩形纸片ABCD沿EF折叠(E、F分别是AD、BC上的点),使点B与四边形CDEF内一点B′重合,若∠B′FC=50°,则∠AEF等于( )| A、110° | B、115° | C、120° | D、130° |

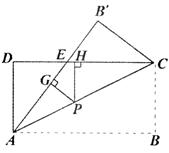
 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么 的度数为 。
的度数为 。