题目内容
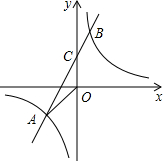 (2013•肇庆一模)如图,已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=
(2013•肇庆一模)如图,已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=| m | x |
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积.
分析:(1)根据m=xy=1×4=n×(-2),求m、n的值,再根据“两点法”求一次函数解析式;
(2)根据一次函数解析式求C点坐标,确定△AOC的底边OC,则A点的横坐标的绝对值为高,由此求出△AOC的面积.
(2)根据一次函数解析式求C点坐标,确定△AOC的底边OC,则A点的横坐标的绝对值为高,由此求出△AOC的面积.
解答:解:(1)由反比例函数解析式可知,m=xy=1×4=n×(-2),解得m=4,n=-2,
将A(-2,-2),B(1,4)代入y=kx+b中,得
,解得
,
∴反比例函数解析式为y=
,一次函数解析式为y=2x+2;
(2)由直线y=2x+2,得C(0,2),
∴S△AOC=
×2×2=2.
将A(-2,-2),B(1,4)代入y=kx+b中,得
|
|
∴反比例函数解析式为y=
| 4 |
| x |
(2)由直线y=2x+2,得C(0,2),
∴S△AOC=
| 1 |
| 2 |
点评:本题主要考查了待定系数法求反比例函数与一次函数的解析式和反比例函数y=
中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
| k |
| x |

练习册系列答案
相关题目
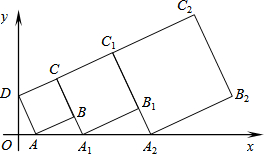 (2013•肇庆一模)在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2013个正方形的面积为( )
(2013•肇庆一模)在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2013个正方形的面积为( )