题目内容
 如图,在等边△ABC中,D为三角形内一点,且BD=3,DA=4,DC=5.将△BDA绕点B沿顺时针旋转60°,使D到D′,则∠BD′C的度数为( )
如图,在等边△ABC中,D为三角形内一点,且BD=3,DA=4,DC=5.将△BDA绕点B沿顺时针旋转60°,使D到D′,则∠BD′C的度数为( )分析:连接DD′,先根据旋转的性质得出∠DBD′=60°,BD=BD′,DA=D′C=4,由等边三角形的判定可知△BDD′是等边三角形,则∠BD′D=60°,DD′=BD=3,再根据勾股定理的逆定理得出∠CD′D=90°,从而求出∠BD′C的度数.
解答: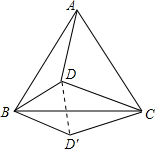 解:连接DD′.
解:连接DD′.
∵将△BDA绕点B沿顺时针旋转60°,使D到D′,
∴∠DBD′=60°,BD=BD′,DA=D′C=4,
∴△BDD′是等边三角形,
∴∠BD′D=60°,DD′=BD=3,
∵D′C=4,CD=5,
∴DD′2+D′C2=CD2,
∴∠CD′D=90°,
∴∠BD′C=∠BD′D+∠CD′D=60°+90°=150°.
故选B.
 解:连接DD′.
解:连接DD′.∵将△BDA绕点B沿顺时针旋转60°,使D到D′,
∴∠DBD′=60°,BD=BD′,DA=D′C=4,
∴△BDD′是等边三角形,
∴∠BD′D=60°,DD′=BD=3,
∵D′C=4,CD=5,
∴DD′2+D′C2=CD2,
∴∠CD′D=90°,
∴∠BD′C=∠BD′D+∠CD′D=60°+90°=150°.
故选B.
点评:本题考查了旋转的性质,等边三角形的判定与性质,勾股定理的逆定理,难度中等,通过作辅助线,得到△BDD′是等边三角形是解题的关键.

练习册系列答案
相关题目
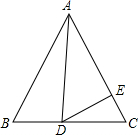 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
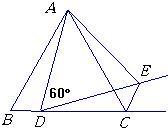 16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是
16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是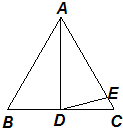 21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°.
21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°.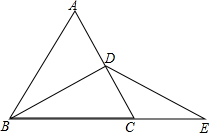 如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm.
如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm. 如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证:
如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证: