题目内容
若等腰梯形的上底和腰长都是3,下底长是5,则这个等腰梯形的中位线长为________;面积是________.
2 8
8
分析:根据梯形的中位线得出梯形ABCD的中位线长是 (AD+BC),代入求出即可;过A作AE⊥BC于E,过D作DF⊥BC于F,得出矩形AEFD和直角三角形,求出BE,根据勾股定理求出AE,代入梯形ABCD的面积公式求出即可.
(AD+BC),代入求出即可;过A作AE⊥BC于E,过D作DF⊥BC于F,得出矩形AEFD和直角三角形,求出BE,根据勾股定理求出AE,代入梯形ABCD的面积公式求出即可.
解答:根据梯形的中位线定理得:梯形ABCD的中位线长是 (AD+BC)=
(AD+BC)= ×(3+5)=4,
×(3+5)=4,

过A作AE⊥BC于E,过D作DF⊥BC于F,
则AE∥DF,∠AEF=90°,
∵AD∥BC,
∴四边形AEFD是矩形,
∴AD=EF=3,AE=DF,
在Rt△AEB和Rt△DFC中,由勾股定理得:BE=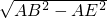 ,CF=
,CF= ,
,
∵AB=DC,
∴BE=CF= (5-3)=1,
(5-3)=1,
在Rt△AEB中,由勾股定理得:AE=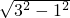 =2
=2 ,
,
∴梯形ABCD的面积是 ×(AD+BC)×AE=
×(AD+BC)×AE= ×(3+5)×2
×(3+5)×2 =8
=8 ,
,
故答案为:2 ,8
,8 .
.
点评:本题考查了梯形的中位线,等腰梯形的性质,矩形的性质和判定,勾股定理等知识点的应用.
 8
8
分析:根据梯形的中位线得出梯形ABCD的中位线长是
 (AD+BC),代入求出即可;过A作AE⊥BC于E,过D作DF⊥BC于F,得出矩形AEFD和直角三角形,求出BE,根据勾股定理求出AE,代入梯形ABCD的面积公式求出即可.
(AD+BC),代入求出即可;过A作AE⊥BC于E,过D作DF⊥BC于F,得出矩形AEFD和直角三角形,求出BE,根据勾股定理求出AE,代入梯形ABCD的面积公式求出即可.解答:根据梯形的中位线定理得:梯形ABCD的中位线长是
 (AD+BC)=
(AD+BC)= ×(3+5)=4,
×(3+5)=4,
过A作AE⊥BC于E,过D作DF⊥BC于F,
则AE∥DF,∠AEF=90°,
∵AD∥BC,
∴四边形AEFD是矩形,
∴AD=EF=3,AE=DF,
在Rt△AEB和Rt△DFC中,由勾股定理得:BE=
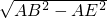 ,CF=
,CF= ,
,∵AB=DC,
∴BE=CF=
 (5-3)=1,
(5-3)=1,在Rt△AEB中,由勾股定理得:AE=
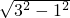 =2
=2 ,
,∴梯形ABCD的面积是
 ×(AD+BC)×AE=
×(AD+BC)×AE= ×(3+5)×2
×(3+5)×2 =8
=8 ,
,故答案为:2
 ,8
,8 .
.点评:本题考查了梯形的中位线,等腰梯形的性质,矩形的性质和判定,勾股定理等知识点的应用.

练习册系列答案
相关题目
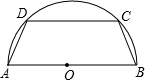 (2007•安溪县质检)如图,有一块半径为5cm的半圆形钢板,计划截成等腰梯形ABCD的形状,他的下底AB是⊙O的直径,上底CD的端点在圆周上.
(2007•安溪县质检)如图,有一块半径为5cm的半圆形钢板,计划截成等腰梯形ABCD的形状,他的下底AB是⊙O的直径,上底CD的端点在圆周上.