Question

17、如图，请写出等腰梯形ABCD（AD∥BC）特有而一般梯形不具有的两个特征：①

等腰梯形的两条对角线相等

；②

同一底上的两底角相等

．

Answer 1

分析：②首先作辅助线D做DE∥AB，把梯形转化成平行四边形和等腰三角形，根据性质即可得出答案．①过D做DM∥AC得到?ACMD和△DMB，证△ABC≌△DCB得到∠DBC=∠ACB=∠M，根据等角对等边即可得出AC=BD．

解答：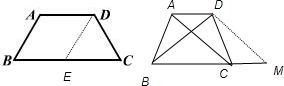
①证明：过D做DM∥AC交BC的延长线于M，
∵AD∥CB，DM∥AC，
∴四边形ACMD是平行四边形，
∴AC=DM，∠ACB=∠M，
∵AD∥BC，AB=DC，
∴∠ABC=∠DCB，
∵BC=BC，AB=DC，
∴△ABC≌△DCB，
∴∠DBC=∠ACB，
∴∠DBC=∠M，
∴DB=DM，
即：AC=BD．
故答案为：等腰梯形的对角线相等．
证明：②过D做DE∥AB交BC于E，
∵AD∥BC，DE∥AB，
∴四边形ABED是平行四边形，
AB=DE，∠B=∠DEC，
∵AB=CD，
∴∠DEC=∠C，
∴∠B=∠C，
故答案为：在同一底上的两底角相等．

点评：本题主要考查了平行四边形的性质和判定，全等三角形的性质和判定，等腰三角形的性质和判定等知识点，解此题的关键是作辅助线把梯形转化成平行四边形和等腰三角形．