题目内容
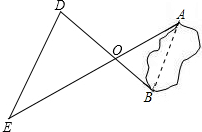
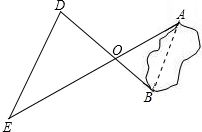如图，一位测量人员，要测量池塘的宽度AB的长，他过A、B两点画两条相交于点O的射线，在射线上取两点D、E，使| OD |
| OB |
| OE |
| OA |
| 1 |
| 3 |
分析：先判定出△AOB和△EOD相似，再根据相似三角形对应边成比例计算即可得解．
解答：解：∵
=
，∠AOB=∠EOD（对顶角相等），
∴△AOB∽△EOD，
∴
=
=
，
∴
=
，
解得AB=111.6米．
所以，可以求出A、B之间的距离为111.6米．
| OD |
| OB |
| OE |
| OA |
∴△AOB∽△EOD，
∴
| DE |
| AB |
| OE |
| OA |
| 1 |
| 3 |
∴
| 37.2 |
| AB |
| 1 |
| 3 |
解得AB=111.6米．
所以，可以求出A、B之间的距离为111.6米．
点评：本题考查了相似三角形的应用，主要利用了相似三角形的判定与相似三角形对应边成比例的性质．
练习册系列答案
相关题目
