题目内容
（11·十堰）关于x,y的二元一次方程组
的解是正整数，则整数P的值为 。
的解是正整数，则整数P的值为 。5或7
首先用含p的代数式分别表示x，y，再根据条件二元一次方程组的解为正整数，得到关于p的不等式组，求出p的取值范围，再根据p为整数确定p的值．
解：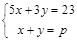
，
②×3得：3x+3y=3p，③，
①-③得：2x=23-3p，
x=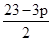
，
②×5得：5x+5y=5p，④，
④-①得：2y=5p-23，
y=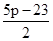
，
∵x，y是正整数，
∴，
解得：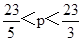
，
∵p为整数，
∴p=5，6，7，
又∵x，y是正整数，
∴p=6时，不合题意舍去，
∴p=5或7，
故答案为：5或7．
解：
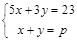，②×3得：3x+3y=3p，③，
①-③得：2x=23-3p，
x=
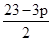，②×5得：5x+5y=5p，④，
④-①得：2y=5p-23，
y=
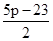，∵x，y是正整数，
∴，
解得：
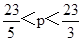，∵p为整数，
∴p=5，6，7，
又∵x，y是正整数，
∴p=6时，不合题意舍去，
∴p=5或7，
故答案为：5或7．
练习册系列答案
相关题目
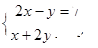的解是（ ）．
的解是 ． 
( )
的正整数解有
的解是___________.
学生推出“林州红旗渠一日游”活动，收费标准如下：