题目内容
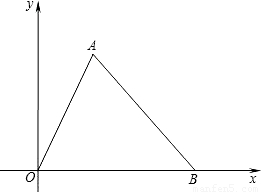
(2002•常州)阅读函数图象,并根据你所获得的信息回答问题:(1)折线OAB表示某个实际问题的函数图象,请你编写一道符合该图象意义的应用题;
(2)根据你给出的应用题分别指出x轴,y轴所表示的意义,并写出A,B两点的坐标;
(3)求出图象AB的函数解析式,并注明自变量x的取值范围.

【答案】分析:应选取常见的量,比如横轴表示时间,纵轴表示离家的路程,这段函数大致可理解为到一个地方去,到后立即返回到家.
解答:解:(1)张老师从家出发,乘车去学校,汽车的速度是每小时25千米,经过2小时到达,到校后因家中有事,立即骑车返回,5小时到家;
(2)x轴表示时间,单位为时,y轴表示离家的路程,单位是千米,那么A(2,50),B(7,0);
(3)设过A,B的解析式为y=kx+b,那么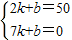 ,
,
解得: ,
,
∴y=-10x+70(2≤x≤7).
点评:本题考查函数图象的应用,需注意选取常见的量,后一段函数的用时较少.
解答:解:(1)张老师从家出发,乘车去学校,汽车的速度是每小时25千米,经过2小时到达,到校后因家中有事,立即骑车返回,5小时到家;
(2)x轴表示时间,单位为时,y轴表示离家的路程,单位是千米,那么A(2,50),B(7,0);
(3)设过A,B的解析式为y=kx+b,那么
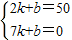 ,
,解得:
 ,
,∴y=-10x+70(2≤x≤7).
点评:本题考查函数图象的应用,需注意选取常见的量,后一段函数的用时较少.

练习册系列答案
相关题目
(2002•常州)图1是棱长为a的小正方体,图2,图3由这样的小正方体摆放而成,按照这样的方法继续摆放,自上而下分别叫第一层,第二层,…第n层,第n层的小正方体的个数记为s,解答下列问题:

(1)按照要求填表:
(2)写出当n=10时,s=______.
(3)据上表中的数据,把s作为纵坐标,n作为横坐标,n作为横坐标,在平面直角坐标系中描出相应的各点.
(4)请你猜一猜上述各点会在某一个函数图象上吗?如果在某一函数的图象上,求出该函数的解析式.

(1)按照要求填表:
| n | 1 | 2 | 3 | 4 | … |
| s | 1 | 3 | 6 | … |
(3)据上表中的数据,把s作为纵坐标,n作为横坐标,n作为横坐标,在平面直角坐标系中描出相应的各点.

(4)请你猜一猜上述各点会在某一个函数图象上吗?如果在某一函数的图象上,求出该函数的解析式.