题目内容
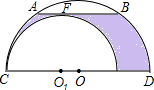 如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于点F,且AB∥CD,AB=6cm,CD=12cm,则图中阴影部分的面积是
如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于点F,且AB∥CD,AB=6cm,CD=12cm,则图中阴影部分的面积是
- A.
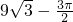
- B.

- C.
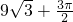
- D.
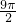
A
分析:将⊙O1移动到O1与O重合,则F和F′重合,连接OB,得出阴影部分的面积是:S= (π×OB2-π×OF′2)-(S扇形AOB-S三角形AOB),求出OF′⊥AB,由垂径定理求出AF′=BF′=3cm,代入即可得出答案.
(π×OB2-π×OF′2)-(S扇形AOB-S三角形AOB),求出OF′⊥AB,由垂径定理求出AF′=BF′=3cm,代入即可得出答案.
解答: 将⊙O1移动到O1与O重合,则F和F′重合,连接OB,AO,
将⊙O1移动到O1与O重合,则F和F′重合,连接OB,AO,
∵AB∥CD,AB=6cm,CD=12cm,AB切⊙O1于F,
∴OF⊥AB,
∴OF′⊥AB,
∴由垂径定理得:AF′=BF′=3cm,
在Rt△BOF′中,BF′=3cm,BO= CD=6cm,
CD=6cm,
即BF′= OB,
OB,
∵∠BOF′=30°,由勾股定理得:OF′=3 cm,
cm,
同理∠AOF′=30°,
∴∠AOB=60°,
∴阴影部分的面积是S= (π×OB2-π×OF′2)-(S扇形AOB-S△AOB)
(π×OB2-π×OF′2)-(S扇形AOB-S△AOB)
= π×(OB2-OF′2)-
π×(OB2-OF′2)- +
+ ×6×3
×6×3
= π×BF′2-6π+9
π×BF′2-6π+9
= π×9-6π+9
π×9-6π+9
=(9 -
- π)cm2.
π)cm2.
故选A.
点评:本题考查了勾股定理,垂径定理,切线性质等知识点,解此题关键是得出阴影部分的面积S= (π×OB2-π×OF′2)-(S扇形AOB-S三角形AOB)=
(π×OB2-π×OF′2)-(S扇形AOB-S三角形AOB)= π×BF′2-(S扇形AOB-S三角形AOB),题目比较典型,是一道比较好的题目.
π×BF′2-(S扇形AOB-S三角形AOB),题目比较典型,是一道比较好的题目.
分析:将⊙O1移动到O1与O重合,则F和F′重合,连接OB,得出阴影部分的面积是:S=
 (π×OB2-π×OF′2)-(S扇形AOB-S三角形AOB),求出OF′⊥AB,由垂径定理求出AF′=BF′=3cm,代入即可得出答案.
(π×OB2-π×OF′2)-(S扇形AOB-S三角形AOB),求出OF′⊥AB,由垂径定理求出AF′=BF′=3cm,代入即可得出答案.解答:
 将⊙O1移动到O1与O重合,则F和F′重合,连接OB,AO,
将⊙O1移动到O1与O重合,则F和F′重合,连接OB,AO,∵AB∥CD,AB=6cm,CD=12cm,AB切⊙O1于F,
∴OF⊥AB,
∴OF′⊥AB,
∴由垂径定理得:AF′=BF′=3cm,
在Rt△BOF′中,BF′=3cm,BO=
 CD=6cm,
CD=6cm,即BF′=
 OB,
OB,∵∠BOF′=30°,由勾股定理得:OF′=3
 cm,
cm,同理∠AOF′=30°,
∴∠AOB=60°,
∴阴影部分的面积是S=
 (π×OB2-π×OF′2)-(S扇形AOB-S△AOB)
(π×OB2-π×OF′2)-(S扇形AOB-S△AOB)=
 π×(OB2-OF′2)-
π×(OB2-OF′2)- +
+ ×6×3
×6×3
=
 π×BF′2-6π+9
π×BF′2-6π+9
=
 π×9-6π+9
π×9-6π+9
=(9
 -
- π)cm2.
π)cm2.故选A.
点评:本题考查了勾股定理,垂径定理,切线性质等知识点,解此题关键是得出阴影部分的面积S=
 (π×OB2-π×OF′2)-(S扇形AOB-S三角形AOB)=
(π×OB2-π×OF′2)-(S扇形AOB-S三角形AOB)= π×BF′2-(S扇形AOB-S三角形AOB),题目比较典型,是一道比较好的题目.
π×BF′2-(S扇形AOB-S三角形AOB),题目比较典型,是一道比较好的题目. 
练习册系列答案
相关题目
 ,n个小半圆弧长的和为
,n个小半圆弧长的和为 ,则
,则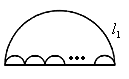
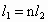



 ,n个小半圆弧长的和为
,n个小半圆弧长的和为 ,则
,则



