题目内容
 (2012•深圳)如图,双曲线y=
(2012•深圳)如图,双曲线y=| k | x |
4
4
.分析:由于⊙O和y=
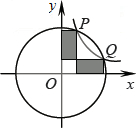
(k>0)都关于y=x对称,于是易求Q点坐标是(3,1),那么阴影面积等于两个面积相等矩形的面积减去一个边长是1的正方形的面积.
| k |
| x |
解答: 解:∵⊙O在第一象限关于y=x对称,
解:∵⊙O在第一象限关于y=x对称,
y=
(k>0)也关于y=x对称,
P点坐标是(1,3),
∴Q点的坐标是(3,1),
∴S阴影=1×3+1×3-2×1×1=4.
故答案是4.
 解:∵⊙O在第一象限关于y=x对称,
解:∵⊙O在第一象限关于y=x对称,y=
| k |
| x |
P点坐标是(1,3),
∴Q点的坐标是(3,1),
∴S阴影=1×3+1×3-2×1×1=4.
故答案是4.
点评:本题考查了反比例函数的性质,解题的关键是知道反比例函数在k>0时关于y=x对称.

练习册系列答案
相关题目
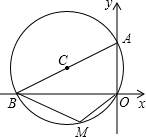 (2012•深圳)如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内
(2012•深圳)如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内
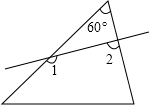 (2012•深圳)如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )
(2012•深圳)如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )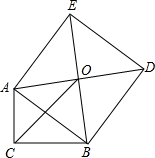 (2012•深圳)如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
(2012•深圳)如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6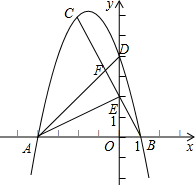 (2012•深圳)如图,已知△ABC的三个顶点坐标分别为A(-4,0)、B(1,0)、C(-2,6).
(2012•深圳)如图,已知△ABC的三个顶点坐标分别为A(-4,0)、B(1,0)、C(-2,6).