Question

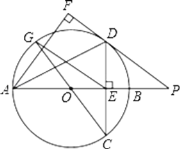
【题目】如图，在△ABC中，AB＝AC，以边AB为直径的⊙O交边BC于点D，交边AC于点E．过D点作DF⊥AC于点F．

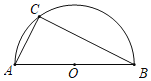
（1）求证：DF是⊙O的切线；

（2）求证：CF＝EF；

（3）延长FD交边AB的延长线于点G，若EF＝3，BG＝9时，求⊙O的半径．

Answer 1

【答案】（1）见解析；（2）见解析；（3）

【解析】

（1）证明OD∥AC，可得OD⊥DF，可得结论；
（2）证出∠CED＝∠C，则CD＝DE，可得出结论；
（3）证出△ODG∽△AFG，得出比例式，即可求出圆的半径.

（1）证明：如图1，连接OD，

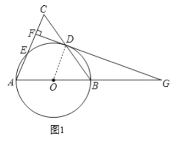
∵AB＝AC，

∴∠ABC＝∠C，

∵OB＝OD，

∴∠ABC＝∠ODB，

∴∠C＝∠ODB，

∴OD∥AC，

∵DF⊥AC，

∴DF⊥OD，

∴DF是⊙O的切线；（亦有其他证法）

（2）证明：如图2，连接DE，

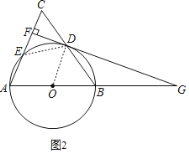
∵四边形AEDB为圆内接四边形，

∴∠CED＝∠ABC，

∵∠ABC＝∠C，

∴∠CED＝∠C，

∴CD＝DE，

∵DF⊥CE，

∴CF＝EF；

（3）如图3，连接AD，

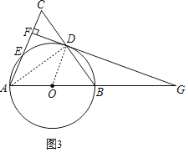
∵AB为⊙O的直径，

∴∠ADB＝90°，

∵AB＝AC，

∴CD＝BD，

∵OD∥AC，

∴△GOD∽△GAF，

∴，

∴设⊙O的半径是r，则AB＝AC＝2r，

∴AF＝2r﹣3，OG＝9+r，AG＝9+2r，

∴，

∴r＝，即⊙O的半径是．