题目内容
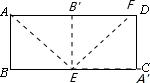 18、当身边没有量角器时,可以通过动手操作得到一些特定的角度.如图,已知矩形ABCD,按如下步骤操作可以得到一个特定的角度.(1)以过点A所在的直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于点E.(2)将纸片返回展平后,再一次折叠纸片,以过点E所在的直线为折痕,使点A落在BC上,折痕EF交AD于点F,则∠DFE=
18、当身边没有量角器时,可以通过动手操作得到一些特定的角度.如图,已知矩形ABCD,按如下步骤操作可以得到一个特定的角度.(1)以过点A所在的直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于点E.(2)将纸片返回展平后,再一次折叠纸片,以过点E所在的直线为折痕,使点A落在BC上,折痕EF交AD于点F,则∠DFE=112.5
度.分析:要想求出∠EFD的度数,可根据折叠的性质的,折叠的角与其对应的折叠角对应相等,由此可得∠AEF=∠A'EF,∠BEA=∠AEB',BE=B'E,AE=EA'(其中A'、B'分别为A、B折叠后对应的点),又有BE=B'E,∠ABE=∠AB'E=90°,可得AE为∠BAB'的角平分线,所以可求的∠BEB'的度数,由于B、E、A'三点在同一直线上,所以可求的∠FEA'的度数,又AD∥BC,∠FEA'和∠DFE是同旁内角,所以可求的∠DFE的度数.
解答:解:折叠的图象如图示: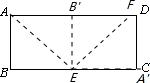 ,
,
则由折叠定理得∠AEF=∠A'EF,∠BEA=∠AEB',BE=B'E,AE=EA',
∵∠ABE=∠AB'E=90°,
∴AE为∠BAB'的角平分线,
∴∠BEA=∠AEB'=45°,
又∠BEA+∠AEB'+∠FEA'=180°,
∴∠FEA'=67.5°,
∴AD∥BC,
∴∠FEA'+∠DFE=180°,
∴∠DFE=112.5°.
故填112.5.
 ,
,则由折叠定理得∠AEF=∠A'EF,∠BEA=∠AEB',BE=B'E,AE=EA',
∵∠ABE=∠AB'E=90°,
∴AE为∠BAB'的角平分线,
∴∠BEA=∠AEB'=45°,
又∠BEA+∠AEB'+∠FEA'=180°,
∴∠FEA'=67.5°,
∴AD∥BC,
∴∠FEA'+∠DFE=180°,
∴∠DFE=112.5°.
故填112.5.
点评:本题考查的是折叠的性质及平行线的性质,折叠的角与其对应的折叠角对应相等,平行线的互为同旁内角的角相加为180°,注意数形结合,是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


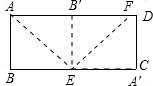 当身边没有量角器时,可以通过动手操作得到一些特定的角度.如图,已知矩形ABCD,按如下步骤操作可以得到一个特定的角度.(1)以过点A所在的直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于点E.(2)将纸片返回展平后,再一次折叠纸片,以过点E所在的直线为折痕,使点A落在BC上,折痕EF交AD于点F,则∠DFE=______度.
当身边没有量角器时,可以通过动手操作得到一些特定的角度.如图,已知矩形ABCD,按如下步骤操作可以得到一个特定的角度.(1)以过点A所在的直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于点E.(2)将纸片返回展平后,再一次折叠纸片,以过点E所在的直线为折痕,使点A落在BC上,折痕EF交AD于点F,则∠DFE=______度.