题目内容
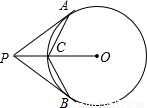
（1998•杭州）如图，AB是⊙O内过点P的一条弦，已知⊙O的半径为3cm，且PA=
cm，PB=
cm，求PO的长．
【答案】分析：过点O作OQ⊥AB于点Q，连接OA、OB，由已知可求得AB的长，从而求得AQ、OQ、PQ，再根据勾股定理求得OP的长．
解答：
解：过点O作OQ⊥AB于点Q，连接OA，OB
∵PA=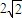
cm，PB=
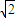cm
∴AB=3
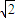cm
∵OA=OB=3cm
∴AQ=
AB=
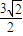cm，
∴OQ=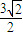
cm，PQ=
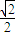cm
∴PO=
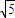cm．
点评：此题主要考查学生垂径定理，把圆中有关弦、弦长、弦心距的计算转化为解直角三角形的计算．
解答：
解：过点O作OQ⊥AB于点Q，连接OA，OB∵PA=
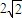cm，PB=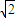cm∴AB=3
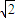cm∵OA=OB=3cm
∴AQ=
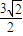AB=cm，∴OQ=
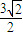cm，PQ=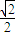cm∴PO=
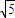cm．点评：此题主要考查学生垂径定理，把圆中有关弦、弦长、弦心距的计算转化为解直角三角形的计算．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
的图象经平移而得到的，此时抛物线过点A（1，0）和x轴上点A右侧的点B，顶点为P．
的图象经平移而得到的，此时抛物线过点A（1，0）和x轴上点A右侧的点B，顶点为P．
，BP=3，求AB的长．
