Question

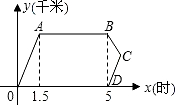
“五一”假期小明骑自行车去郊游，早上8：00从家出发，9：30到达目的地．在郊游地点玩了3个半小时后按原路以原速返回，同时爸爸骑电动车从家出发沿同一路线迎接他，爸爸骑电动车的速度是20千米/小时，小明骑自行车的速度是10千米/小时．设小明离开家的时间为x小时，下图是他们和家的距离y（千米）与x（时）的函数关系图象．
（1）目的地与家相距千米；
（2）设爸爸与家的距离为y₁（千米），求爸爸从出发到与小明相遇的过程中，y₁与x的函数关系式（不要求写出自变量x的取值范围）；
（3）设小明与家的距离为y₂（千米），求小明从返程到与爸爸相遇的过程中，y₂与x的函数关系式（不要求写出自变量x的取值范围）；
（4）说明点C的实际意义，并求出此时小明与家的距离．

Answer 1

解：方法一：
（1）10×1.5=15（千米）
（2）y₁=20（x-5）
即y₁=20x-100
（3）y₂=15-10（x-5）
即y₂=-10x+65．
（4）点C表示小明与爸爸相遇．
当小明与爸爸相遇时，y₁=y₂．
即20x-100=-10x+65．
解得，x=5．
当x=5时，y₂=-10×5+65=10（千米）．
所以此时小明离家还有10千米．

方法二：
（1）15
（2）小明从郊游地点返回，到与爸爸相遇所用时间：15÷（10+20）=（小时）
相遇时，爸爸与家的距离为：20×=10（千米）
所以，点C的坐标为（5，10）．
又由题意，得D点坐标（5，0）．
所以易求直线DC的表达式：y₁=20x-100．
（3）因为点C的坐标为（5，10），B点坐标（5，15），
易求直线BC的表达式：y₂=-10x+65．
（4）点C表示小明与爸爸相遇．
因为C点坐标为（5，10），
所以此时小明离家还有10千米．
分析：（1）小明骑自行车的速度是10千米/小时，他到达目的地花了1.5小时，所以目的地与家相距15千米．
（2）爸爸的出发时间是（x-5），爸爸与家的距离是爸爸的速度与行驶时间（x-5）成正比例关系，即可求出y₁与x的函数关系式．
（3）小明与家的距离=目的地与家的距离-小明返回时所行驶的距离．
（4）点C表示小明与爸爸相遇，当他们相遇时，小明与家的距离=爸爸与家的距离，即y₁=y₂，解出相遇的时间，则小明与家的距离可求解．
点评：本题重点考查了一次函数图象和实际应用相结合的问题，要求学生具备在直角坐标系中的读图能力．