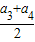题目内容
(2008•大兴安岭)为紧急安置100名地震灾民,需要同时搭建可容纳6人和4人的两种帐篷,则恰好能安置的搭建方案共有( )A.8种
B.9种
C.16种
D.17种
【答案】分析:可设6人的帐篷有x顶,4人的帐篷有y顶.根据两种帐篷容纳的总人数为100人,可列出关于x、y的二元一次方程,根据x、y均为非负整数,求出x、y的取值.根据未知数的取值即可判断出有几种搭建方案.
解答:解:设6人的帐篷有x顶,4人的帐篷有y顶,
依题意,有:6x+4y=100,整理得y=25-1.5x,
因为x、y均为非负整数,所以25-1.5x≥0,解得0<x≤16 ,
,
从2到16的偶数共有8个,
所以x的取值共有8种可能,
即共有8种搭建方案.故选A.
点评:解决本题的关键是找到人数的等量关系,及帐篷数的不等关系.
解答:解:设6人的帐篷有x顶,4人的帐篷有y顶,
依题意,有:6x+4y=100,整理得y=25-1.5x,
因为x、y均为非负整数,所以25-1.5x≥0,解得0<x≤16
 ,
,从2到16的偶数共有8个,
所以x的取值共有8种可能,
即共有8种搭建方案.故选A.
点评:解决本题的关键是找到人数的等量关系,及帐篷数的不等关系.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
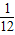 x+11,假设群众上下船的时间不计,求冲锋舟在距离A
x+11,假设群众上下船的时间不计,求冲锋舟在距离A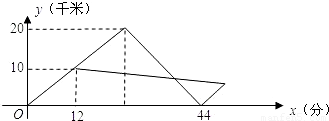 地多远处与救生艇第二次相遇?
地多远处与救生艇第二次相遇?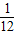 x+11,假设群众上下船的时间不计,求冲锋舟在距离A
x+11,假设群众上下船的时间不计,求冲锋舟在距离A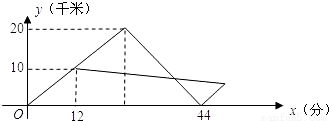 地多远处与救生艇第二次相遇?
地多远处与救生艇第二次相遇?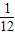 x+11,假设群众上下船的时间不计,求冲锋舟在距离A
x+11,假设群众上下船的时间不计,求冲锋舟在距离A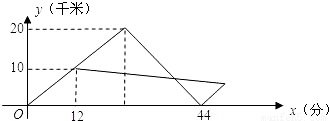 地多远处与救生艇第二次相遇?
地多远处与救生艇第二次相遇?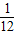 x+11,假设群众上下船的时间不计,求冲锋舟在距离A
x+11,假设群众上下船的时间不计,求冲锋舟在距离A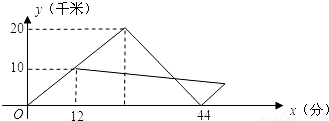 地多远处与救生艇第二次相遇?
地多远处与救生艇第二次相遇?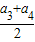
 a,
a,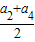
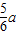 ,
,