Question

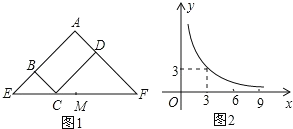
【题目】如图，□ABCD中，AB=6，E是BC边的中点，F为CD边上一点，DF=4.8，∠DFA=2∠BAE，则AF 的长为（ ）

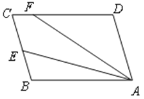
A. 4.8B. 6C. 7.2D. 10.8

Answer 1

【答案】C

【解析】

在AF上截取AG=AB，连接EG，CG．利用全等三角形的判定定理SAS证得△AEG≌△AEB，由全等三角形的对应角相等、对应边相等知EG=BE，∠B=∠AGE；然后由中点E的性质平行线的性质以及等腰三角形的判定与性质求得CF=FG；最后根据线段间的和差关系证得结论．

在AF上截取AG=AB，连接EG，CG．

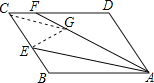
∵四边形ABCD是平行四边形，

∴AB∥CD，CD=AB=6，

∴∠DFA=∠BAF，

∵∠DFA=2∠BAE，

∴∠FAE=∠BAE，

在△BAE和△GAE中，

，

∴△BAE≌△GAE（SAS）．

∴EG=BE，∠B=∠AGE；

又∵E为BC中点，

∴CE=BE．

∴EG=EC，

∴∠EGC=∠ECG；

∵AB∥CD，

∴∠B+∠BCD=180°．

又∵∠AGE+∠EGF=180°，∠AGE=∠B，

∴∠BCF=∠EGF；

又∵∠EGC=∠ECG，

∴∠FGC=∠FCG，

∴FG=FC；

∵DF=4.8，

∴CF=CD-DF=6-4.8=1.2，

又∵AG=AB，

∴AF=AG+GF=AB+FC=CD+FC=6+1.2=7.2．

故选C．