题目内容
某市热带植物园的门票价格规定如下表所列、某校七年级(1)、(2)两个班学生共103人去该园参观,其中七(1)班人数不少于30人且不多于50人、经预算,若两班都以班为单位分别购票,则总共付1950元.
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 每人门票价 | 20元 | 18元 | 15元 |
(2)求两班各有多少名学生?
解:(1)最多可以节省:1950-103×15=405(元);
(2)设七年级(1)班有x名学生,七年级(2)班有y名学生,
因为甲班人数不少于30人且不多于50人,
所以依题意,得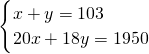 ,
,
解这个方程组,得 ,
,
答:七年级(1)班有48名学生,七年级(2)班有55名学生.
分析:(1)若两班合在一起统一购票,显然票价是每人15元,求得总价,进一步求得节省的票价;
(2)设甲、乙班分别有学生x、y名.因为甲班人数不少于30人且不多于50人,所以乙班人数不小于53人,不大于73人,则甲班的票价是每人20元,乙班的票价是每人18元.根据学生共103人和两班都以班为单位分别购票,则共付1950元,列方程组求解.
点评:本题考查了二元一次方程组的应用,注意理解各段票价的意义,这是解决问题的关键.
(2)设七年级(1)班有x名学生,七年级(2)班有y名学生,
因为甲班人数不少于30人且不多于50人,
所以依题意,得
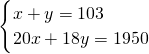 ,
,解这个方程组,得
 ,
,答:七年级(1)班有48名学生,七年级(2)班有55名学生.
分析:(1)若两班合在一起统一购票,显然票价是每人15元,求得总价,进一步求得节省的票价;
(2)设甲、乙班分别有学生x、y名.因为甲班人数不少于30人且不多于50人,所以乙班人数不小于53人,不大于73人,则甲班的票价是每人20元,乙班的票价是每人18元.根据学生共103人和两班都以班为单位分别购票,则共付1950元,列方程组求解.
点评:本题考查了二元一次方程组的应用,注意理解各段票价的意义,这是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(12分)某市热带植物园的门票价格规定如下表所列. 某校七年级(1)、(2)两个班学生共103人去该园参观, 其中七(1)班人数不少于30人且不多于50人. 经预算,若两班都以班为单位分别购票,则总共付1950元.
|
购票人数 |
1~50人 |
51~100人 |
100人以上 |
|
每人门票价 |
20元 |
18元 |
15元 |
(1)若两班学生合在一起作为一个团体购票,则最多可以节省门票多少元?
(2)求两班各有多少名学生?
(12分)某市热带植物园的门票价格规定如下表所列. 某校七年级(1)、(2)两个班学生共103人去该园参观, 其中七(1)班人数不少于30人且不多于50人. 经预算,若两班都以班为单位分别购票,则总共付
某校七年级(1)、(2)两个班学生共103人去该园参观, 其中七(1)班人数不少于30人且不多于50人. 经预算,若两班都以班为单位分别购票,则总共付 1950元.
1950元.
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 每人门票价 | 20元 | 18元 | 15元 |
(2)求两班各有多少名学生?