题目内容
已知实数a、b、c满足a+b+c=0,abc>0,x=
+
+
,y=a(
+
)+b(
+
)+c(
+
),则x+2y+3xy的值等于( )
| a |
| |a| |
| |b| |
| b |
| c |
| |c| |
| 1 |
| b |
| 1 |
| c |
| 1 |
| c |
| 1 |
| a |
| 1 |
| a |
| 1 |
| b |
| A、0 | B、1 | C、2 | D、不确定 |
分析:根据a+b+c=0,abc>0,可得出a,b,c中两负一正,且两个负数的绝对值的和等于这个正数的绝对值,假设a>0,b<0,c<0,即|a|=|b|+|c|,从而代入求出x,y的值,再代入求出x+2y+3xy的值.
解答:解:∵a+b+c=0,abc>0,
∴a+b=-c,a+c=-b,b+c=-a,
∴假设a>0,b<0,c<0,即|a|=|b|+|c|,
∴x=1-1-1=-1,
y=
+
+
+
+
+
=
+
+
=-1-1-1
=-3,
∴x+2y+3xy=-1+2×(-3)+3×(-1)×(-3)=-1-6+9=2.
故选C.
∴a+b=-c,a+c=-b,b+c=-a,
∴假设a>0,b<0,c<0,即|a|=|b|+|c|,
∴x=1-1-1=-1,
y=
| a |
| b |
| a |
| c |
| b |
| c |
| b |
| a |
| c |
| a |
| c |
| b |
=
| a+c |
| b |
| a+b |
| c |
| b+c |
| a |
=-1-1-1
=-3,
∴x+2y+3xy=-1+2×(-3)+3×(-1)×(-3)=-1-6+9=2.
故选C.
点评:本题考查了分式的混合运算以及绝对值的计算,是一道竞赛题,难度较大.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 (2013•菏泽)(1)已知m是方程x2-x-2=0的一个实数根,求代数式
(2013•菏泽)(1)已知m是方程x2-x-2=0的一个实数根,求代数式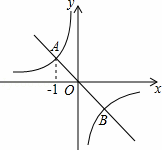
 (1)已知m是方程x2-x-2=0的一个实数根,求代数式
(1)已知m是方程x2-x-2=0的一个实数根,求代数式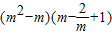 的值.
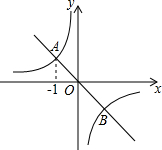
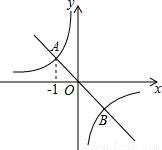
的值.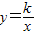 的图象交于A、B两点.
的图象交于A、B两点.