题目内容
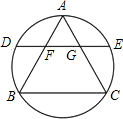 如图,边长为12的正三角形ABC内接于圆,弦DE∥BC分别交AB,AC于F,G,若AF长x,DF长y都是正整数,则y的值为( )
如图,边长为12的正三角形ABC内接于圆,弦DE∥BC分别交AB,AC于F,G,若AF长x,DF长y都是正整数,则y的值为( )| A、2 | B、3 | C、4 | D、6 |
分析:由已知可得DE=x+2y,过O点作OH⊥BC,垂足为H,连接OB,根据已知条件可求半径OB,由DE≤2OB,列不等式,再根据相交弦定理及x、y为正整数求解.
解答: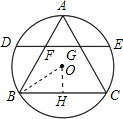 解:过O点作OH⊥BC,垂足为H,连接OB,
解:过O点作OH⊥BC,垂足为H,连接OB,
在Rt△OBH中,BH=
BC=6,∠OBH=
∠ABC=30°,
∴OB=
=4
,
根据圆的对称性及等边三角形的性质可知,DE=x+2y,
由DE≤2OB,得x+2y≤8
≈13.8,
又由相交弦定理,得AF×BF=DF×FE,
即x(12-x)=y(x+y),
当x=1时,方程为y2+y-11=0,y无正整数解,
当x=2时,方程为y2+2y-20=0,y无正整数解,
当x=3时,方程为y2+3y-27=0,y无正整数解,
当x=4时,方程为y2+4y-32=0,y=-8或4(舍去负数),
而x=4,y=4满足x+2y≤8
,
故选C.
 解:过O点作OH⊥BC,垂足为H,连接OB,
解:过O点作OH⊥BC,垂足为H,连接OB,在Rt△OBH中,BH=
| 1 |
| 2 |
| 1 |
| 2 |
∴OB=
| BH |
| cos30° |
| 3 |
根据圆的对称性及等边三角形的性质可知,DE=x+2y,
由DE≤2OB,得x+2y≤8
| 3 |
又由相交弦定理,得AF×BF=DF×FE,
即x(12-x)=y(x+y),
当x=1时,方程为y2+y-11=0,y无正整数解,
当x=2时,方程为y2+2y-20=0,y无正整数解,
当x=3时,方程为y2+3y-27=0,y无正整数解,
当x=4时,方程为y2+4y-32=0,y=-8或4(舍去负数),
而x=4,y=4满足x+2y≤8
| 3 |
故选C.
点评:本题考查了三角形外接圆的性质,等边三角形的性质,相交弦定理的运用.关键是明确DE的取值范围,根据x、y为正整数,分类讨论.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
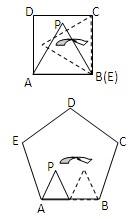 16、如图,已知正方形ABCD的边长AB=1,正△PAE的边长AE=1,开始时正△PAE与正方形ABCD边AB重合,顶点P在正方形内,将正△PAE在正方形内按如图所示的方式,沿着正方形的边AB、BC、CD、DA、AB、BC…连续地翻转
16、如图,已知正方形ABCD的边长AB=1,正△PAE的边长AE=1,开始时正△PAE与正方形ABCD边AB重合,顶点P在正方形内,将正△PAE在正方形内按如图所示的方式,沿着正方形的边AB、BC、CD、DA、AB、BC…连续地翻转 (2012•丹徒区模拟)用两个边长为1的正六边形拼接成如图(a)的图形,其周长为10;用三个边长为1的正六边形可以拼接成如图(b)或(c)的图形,其周长分别为12和14.若要拼接成周长为18的图形,所需这样的正六边形至少为x个,至多为y个,则x+y=
(2012•丹徒区模拟)用两个边长为1的正六边形拼接成如图(a)的图形,其周长为10;用三个边长为1的正六边形可以拼接成如图(b)或(c)的图形,其周长分别为12和14.若要拼接成周长为18的图形,所需这样的正六边形至少为x个,至多为y个,则x+y=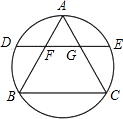 如图,边长为12的正三角形ABC内接于圆,弦DE∥BC分别交AB,AC于F,G,若AF长x,DF长y都是正整数,则y的值为
如图,边长为12的正三角形ABC内接于圆,弦DE∥BC分别交AB,AC于F,G,若AF长x,DF长y都是正整数,则y的值为