题目内容
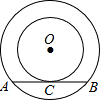如图是同心圆的圆环面，大圆的弦AB切小圆点C，若大圆半径为5cm，小圆半径为3cm，则AB=________cm．
8
分析：连接OA、OC，根据切线的性质可知△OAC是直角三角形，OC垂直平分AB，根据勾股定理及垂径定理即可解答．
解答：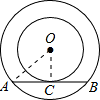
解：连接OA、OC，
∵AB是小圆的切线，∴OC⊥AB，
∵OA=5cm，OC=3cm，
∴AC=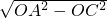
=
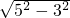=4cm，
∵AB是大圆的弦，OC过圆心，OC⊥AB，
∴AB=2AC=2×4=8cm．
故答案为8．
点评：此类题目比较简单，解答此题的关键是连接OA、OC，构造出直角三角形，利用切线的性质及勾股定理解答．
分析：连接OA、OC，根据切线的性质可知△OAC是直角三角形，OC垂直平分AB，根据勾股定理及垂径定理即可解答．
解答：
解：连接OA、OC，∵AB是小圆的切线，∴OC⊥AB，
∵OA=5cm，OC=3cm，
∴AC=
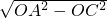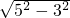==4cm，∵AB是大圆的弦，OC过圆心，OC⊥AB，
∴AB=2AC=2×4=8cm．
故答案为8．
点评：此类题目比较简单，解答此题的关键是连接OA、OC，构造出直角三角形，利用切线的性质及勾股定理解答．
练习册系列答案
53随堂测系列答案
相关题目
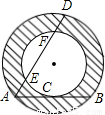
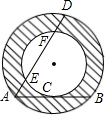如图，一种圆管的横截面是同心圆的圆环面，大圆的弦AB切小圆于点C，大圆的弦AD交小圆于点E和F．为了计算截面的面积，甲、乙、丙三个同学分别用刻度尺测量出有关线段的长度：甲测得AB的长，乙测得AC的长，丙测得AD与EF的长．其中可以算出截面（图中阴影部分）面积的同学是（ ）
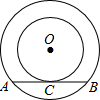（2010•海曙区模拟）如图是同心圆的圆环面，大圆的弦AB切小圆点C，若大圆半径为5cm，小圆半径为3cm，则AB=
