题目内容
【题目】如图，抛物线
（a、b、c为常数，a≠0）经过点A（﹣1，0），B（5，﹣6），C（6，0）．
（1）求抛物线的解析式；
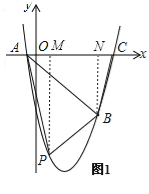
（2）如图，在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大？若存在，请求出点P的坐标；若不存在，请说明理由；
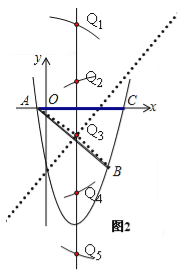
（3）若点Q为抛物线的对称轴上的一个动点，试指出△QAB为等腰三角形的点Q一共有几个？并请求出其中某一个点Q的坐标．
【答案】（1）
；（2）P（2，﹣12）；（3）这样的Q点一共有5个，如：Q3（
，
）．
【解析】（1）设y=a（x+1）（x﹣6）（a≠0），把B（5，﹣6）代入：a（5+1）（5﹣6）=﹣6，a=1，∴y=（x+1）（x﹣6），即；
（2）存在，如图1，分别过P、B向x轴作垂线PM和BN，垂足分别为M、N，设P（m，
），四边形PACB的面积为S，则PM=
，AM=m+1，MN=5﹣m，CN=6﹣5=1，BN=5，∴S=S△AMP+S梯形PMNB+S△BNC=
=
=
当m=2时，S有最大值为48，这时=
=﹣12，∴P（2，﹣12）；
（3）这样的Q点一共有5个，连接Q3A、Q3B，=
；
因为Q3在对称轴上，所以设Q3（，y），∵△Q3AB是等腰三角形，且Q3A=Q3B，由勾股定理得：
，解得：y=，∴Q3（，）．
练习册系列答案
相关题目
