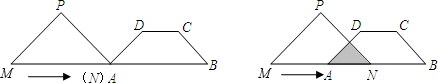Question

 如右图，在等腰梯形ABCD中，AD∥BC，AD=AB.过A作AF⊥BD，交BC于G，延长BC至E，使CE=CD.

1.（1）请指出四边形ACED的形状，并证明；

2.（2）如果BD=8，AG=6，求△BDE的面积.（10分）

 

 

Answer 1

 

1.（1）四边形ACED为平行四边形.（1分）

      在等腰梯形ABCD中，AD=AB=CD=CE, AD//CE（3分）,

      ∴四边形ACED为平行四边形.

2.（2）∵AB=AD ,   ∴∠ADB=∠ABD.

       ∵AD//BC, ∴∠ADB=∠DBC.

       ∴∠ABD=∠DBC（4分）,  而BF=BF， ∠AFB=∠GFB=90⁰.

       ∴△AFB≌△GFB.

       ∴AF=GF=3.（5分）

    又∵AG垂直平分BD, ∴BF=4.

      在Rt△AFB中，得AB=5.（6分）

      由（1）可得AC//DE.所以∠E=∠ACB.

     在等腰梯形ABCD中，易得∠ACB=∠DBC.（7分）

      ∴∠E=∠DBC=∠ABD.

      ∴△ABD∽△DBE .  （8分）

      ∴S_△BDE / S_△ABD=BD²/AB²,而S_△ABD=12.（9分）

      ∴S_△BDE = .（10分）

解析:略