Question

若等腰梯形的对角线互相垂直，高为8cm，则此梯形的面积为

1. A.
   63cm²
2. B.
   64cm²
3. C.
   8cm²
4. D.
   无法确定

Answer 1

B
分析：作DF垂直BE于F，DE∥AC交BE的延长线于点E，故∠BDE-90°，从而得到△BDE为等腰直角三角形，根据三线合一性质可求得BE的长，即上底与下底的和，则根据梯形的面积公式即可得到其面积．故选B．
解答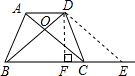：解：作DF垂直BE于F，DE∥AC交BE的延长线于点E．
故∠BDE=90°，DF=8，BD=DE．?∠DBE=∠DEB=45°，
根据等腰三角形的性质可得DF垂直平分BE?BF=FE=DF=8，
梯形面积为：16×8÷2=64cm²．
故选B．
点评：本题考查的是等腰梯形的性质以及平行四边形性质的综合运用．