题目内容
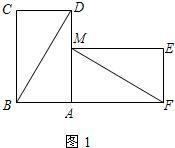
有两张完全重合的矩形纸片,小亮将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连结BD、MF,此时他测得BD=8cm,∠ADB=30°.

1.在图1中,请你判断直线FM和BD是否垂直?并证明你的结论;
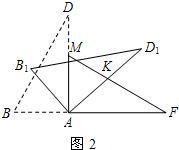
2.小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,请直接写出旋转角β的度数;

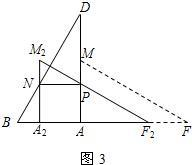
3.若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离是多少.

【答案】
1.垂直. …………………………1分
证明:延长FM交BD于N.
如图1,由题意得:△BAD≌△MAF.
∴∠ADB=∠AFM.
又∵∠DMN=∠AMF,
∴∠ADB+∠DMN=∠AFM+∠AMF=90°.
∴∠DNM=90°,∴BD⊥MF. 2分
2.β的度数为60°或15°(答对一个得1分) 4分
3.如图2,由题意知四边形PNA2A为矩形,设A2A=x,则PN=x.

在Rt△A2M2F2中,∵M2F2=MF=BD=8,∠A2F2M2=∠AFM=∠ADB=30°.
∴M2A2=4,A2F2= . …………………………..5分
. …………………………..5分
∴AF2= -x.
-x.
在Rt△PAF2中,∵∠PF2A=30°.
∴AP=AF2 30°=(
30°=( -x)·
-x)· =4-
=4- x.
x.
∴PD=AD-AP= -4+
-4+ x. ……………..6分
x. ……………..6分
∵NP∥AB,∴ =
=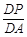 .∴
.∴ =
= ,
,
解得x=6-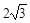 .即平移的距离是(6-
.即平移的距离是(6-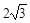 )cm.………………7分
)cm.………………7分
【解析】本题涉及的知识点有三角形全等、旋转和平移、三角函数的有关计算,综合性较强。
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目