Question

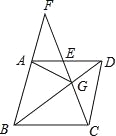
【题目】如图，在菱形ABCD中，G是BD上一点，连接CG并延长交BA的延长线于点F，交AD于点E．

（1）求证：AG=CG．

（2）求证：AG2=GEGF．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

试题分析： （1）连接AC，根据菱形对角线互相垂直平分，G在AC的中垂线上，从而AG=CG；（2）易证△AEG∽△FGA，利用对应边成比例可得到结论.

试题解析：（1）连接AC，在菱形ABCD中，AC、BD为对角线，∴BD垂直平分AC.∵G是BD上一点，∴AG=CG.

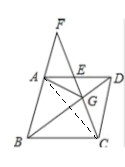
（2）∵AG=GC，∴∠GAC=∠GCA.∵AD=CD，∴∠DAC=∠DCA.∴∠DAC-∠GAC=∠DCA-∠GCA，即∠DCG=∠DAG.，∵AB∥CD，∴∠DCG=∠F，∴∠F=∠DAG.又∵∠AGF=∠AGE，∴△AEG∽△FGA，∴.∴AG2=GEGF．