题目内容
要在半径长为1米、圆心角为60°的扇形AOB铁皮上截取一块尽可能大的正方形.小明设计如下两种截取方案.
方案一(如图1):C在半径OA上,D、E在半径OB上,F在弧AB上;
方案二(如图2):C在OA上,D在OB上,E,F在弧AB上.
请通过计算这两种方案中正方形铁皮的面积帮小明选择合理的方案.(参考数据: )
)
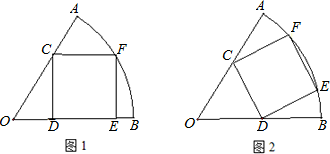
 解:方案一:如图1
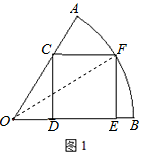
解:方案一:如图1连接OF,设正方形CDEF的边长为x,
∵圆心角为60°,
∴OD=
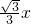 ,
,则在Rt△OFE中,
OF2=OE2+EF2,即12=x2+(x+
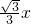 )2,
)2,解得x2=
 ,
,∴S四边形CDEF=x2=
 ≈0.29;
≈0.29;方案二:如图2所示,
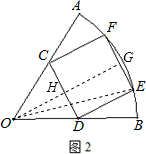
过O作OG⊥EF,交CD于点H,连接OE,
设EG=x,
∵四边形CDEF是正方形,
∴OH⊥CD,
∴EG=DH=x,
∵∠DOC=60°,H为CD中点,
∴OH=
 DH,
DH,∴OG=OH+HG=
 HC+CF=
HC+CF= x+2x,
x+2x,在Rt△OEG中,
OE2=GE2+OG2,即12=x2+(
 x+2x)2,
x+2x)2,解得x2=
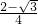 ,
,∴S四边形CDEF=4x2=2-
 ≈0.27,
≈0.27,∴第(一)种方案截取的正方形的面积最大.
分析:根据题意画出图形,分别连接PQ和过O作OG⊥DE,交CF于点H,连接OF,构造直角三角形求得正方形的边长,求得正方形的面积后比较即可.由于正方形内接于扇形,故应分两种情况进行讨论.
点评:本题考查的是垂径定理及勾股定理,解答此题的关键是根据题意画出图形,作出辅助线,构造出直角三角形,再进行解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都要喷洒到水,假设每个喷水龙头的喷洒范围都是半径为6米的圆面,则需安装这种喷水龙头的个数最少是( )
如图,要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都要喷洒到水,假设每个喷水龙头的喷洒范围都是半径为6米的圆面,则需安装这种喷水龙头的个数最少是( )


