题目内容
将直径为64cm的圆形铁皮，做成八个相同圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），那么每个圆锥容器的高为分析：易求得圆锥的侧面积，那么利用圆锥的侧面积=π×底面半径×母线长可求得圆锥的底面半径，利用勾股定理即可求得每个圆锥容器的高．
解答：解：每个圆锥的侧面积为：π×（64÷2）2÷8=128πcm2；
由题意得：128π=π×r×32，解得：r=4cm；
每个圆锥容器的高为：
=12
cm．
由题意得：128π=π×r×32，解得：r=4cm；
每个圆锥容器的高为：
| 322-42 |
| 7 |
点评：关键是求得圆锥的底面半径，注意利用圆锥的高，母线长，底面半径组成直角三角形这个知识点．
练习册系列答案
阅读快车系列答案
相关题目
将直径为64cm的圆形铁皮，做成四个相同圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），那么每个圆锥容器的高为（ ）
A、8
| ||
B、8
| ||
C、16
| ||
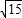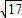| D、16cm |
cm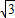
cm
cm