题目内容
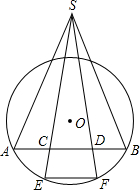
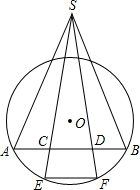如图，已知圆O的弦AB被点C、D三等分，又E、F是弧AB的三等分点，连接EC、FD交于S，连接SA、SB，求证：∠ASB=| 1 | 3 |
分析：可连接OE、OF、AE、AF，延长SA交FE的延长线于K，由于E、F是弧AB的三等分点，即
=
，得出AB∥EF，进而得出对应线段成比例，由线段之间的关系得出∠KAF=90°，得出OE∥SA，以及OF∥SB，进而可求解结论．
 |
| AE |
|
| BF |
解答：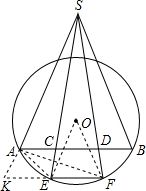
证明：连接OE、OF、AE、AF，延长SA交FE的延长线于K，
∵
=
，
∴AB∥EF，
∴
=
=
，
∵AC=CD，
∴KE=EF=AE，∠KAF=90°，
FA⊥SA，又
=
，
∴OE⊥FA，OE∥SA，
同理可证OF∥SB，
∴∠ASB=∠EOF=
∠AOB．
证明：连接OE、OF、AE、AF，延长SA交FE的延长线于K，∵
|
| AE |
|
| BF |
∴AB∥EF，
∴
| KE |
| AC |
| SE |
| SC |
| EF |
| CD |
∵AC=CD，
∴KE=EF=AE，∠KAF=90°，
FA⊥SA，又
|
| AE |
|
| EF |
∴OE⊥FA，OE∥SA，
同理可证OF∥SB，
∴∠ASB=∠EOF=
| 1 |
| 3 |
点评：本题主要考查了圆心角、弦及弧之间的关系和平行线分线段成比例的性质问题，能够熟练掌握．
练习册系列答案
阅读快车系列答案
相关题目
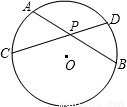
如图，已知圆O的弦AB经过弦CD的中点P，若AP=2cm，CD=6cm，则PB的长为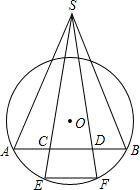
如图，已知圆O的弦AB被点C、D三等分，又E、F是弧AB的三等分点，连接EC、FD交于S，连接SA、SB，求证：∠ASB=
∠AOB．
