Question

如果两个三角形有两个角和第三个角的平分线对应相等，那么这两个三角形全等．

Answer 1

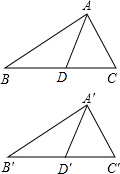解：
∵∠B=∠B′，∠C=∠C′，
∴∠BAC=∠B′A′C′，
∵AD，A′D′分别平分∠BAC，∠B′A′C′，
∴∠BAD=∠B′A′D′∵AD=A′D′，∠B=∠B′，
∴△ABD≌△A′B′D′（AAS），
∴AB=A′B′，
∵∠B=∠B′，AB=A′B′，∠BAC=∠B′A′C′，
∴△ABC≌△A′B′C′（ASA）．
分析：根据题意要证明∴△ABC≌△A′B′C′，首先证明△ABD≌△A′B′D′得到AB=A′B′，进一步证明这两三角形全等．
点评：本题主要考查三角形全等的判定，要熟悉课本上的几种判定定理．