ЬтФПФкШн
ЁОЬтФПЁПМзЁЂввСНГЕДгAЕиГіЗЂбиЭЌвЛТЗЯпЪЛЯђBЕиЃЌМзГЕЯШГіЗЂдШЫйЪЛЯђBЕиЃЎ40ЗжжгКѓЃЌввГЕГіЗЂЃЌдШЫйааЪЛвЛЖЮЪБМфКѓЃЌдкЭОжаЕФЛѕеОзАЛѕКФЪБАыаЁЪБЃЌгЩгкТњдиЛѕЮяЃЌЮЊСЫааЪЛАВШЋЃЌЫйЖШМѕЩйСЫ50ЧЇУз/ЪБЃЌНсЙћгыМзГЕЭЌЪБЕНДяBЕиЃЎМзввСНГЕОрAЕиЕФТЗ ГЬyЃЈЧЇУзЃЉгыввГЕааЪЛЪБМфxЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЎЧыНсКЯЭМЯѓаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉжБНгаДГіaЕФжЕЃЌВЂЧѓМзГЕЕФЫйЖШЃЛ
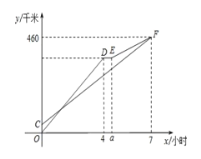
ЃЈ2ЃЉЧѓЭМжаЯпЖЮEFЫљБэЪОЕФyгыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГіздБфСПxЕФШЁжЕЗЖЮЇ.
ЁОД№АИЁПЃЈ1ЃЉa=4.5ЃЌМзЕФЫйЖШЮЊ![]() ЃЈЧЇУз/аЁЪБЃЉЃЈ2ЃЉy=40x+180ЃЈ4.5ЁмxЁм7ЃЉ
ЃЈЧЇУз/аЁЪБЃЉЃЈ2ЃЉy=40x+180ЃЈ4.5ЁмxЁм7ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнввдкЭОжазАЛѕКФЪБАыаЁЪБвзжЊa=4.5ЃЌМзДгAЕНBЙВгУСЫЃЈ![]() +7ЃЉаЁЪБЃЌИљОнЫйЖШЕФЙЋЪНМДПЩЧѓНтЃЛ
+7ЃЉаЁЪБЃЌИљОнЫйЖШЕФЙЋЪНМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЩшвввЛПЊЪМЕФЫйЖШЮЊvЧЇУз/аЁЪБЃЌРћгУввСНЖЮЪБМфФкЕФТЗГЬКЭСаГіЗНГЬЧѓГіvЃЌПЩЕУDЃЌEЕФзјБъЃЌдйИљОнД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіEFЕФНтЮіЪН.
ЃЈ1ЃЉвРЬтвтЕУa=4.5ЃЌ
МзЕФЫйЖШЮЊ![]() ЃЈЧЇУз/аЁЪБЃЉ
ЃЈЧЇУз/аЁЪБЃЉ
ЃЈ2ЃЉвввЛПЊЪМЕФЫйЖШЮЊvЧЇУз/аЁЪБЃЌ
дђ4v+ЃЈ7-4.5ЃЉЃЈv-50ЃЉ=460
НтЕУv=90ЃЈЧЇУз/аЁЪБЃЉ
дђDЃЈ4,360ЃЉЃЌEЃЈ4.5ЃЌ360ЃЉ
ЩшжБЯпEFЕФНтЮіЪНЮЊy=kx+b
АбEЃЈ4.5ЃЌ360ЃЉЃЌFЃЈ7,460ЃЉДњШыЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ЁрЯпЖЮEFЫљБэЪОЕФyгыxЕФКЏЪ§ЙиЯЕЪНЮЊy=40x+180ЃЈ4.5ЁмxЁм7ЃЉ