题目内容
【题目】三角形的一条边与另一条边的反向延长线组成的角,叫做三角形的外角。如图,点D为BC延长线上一点,则∠ACD为△ABC的一个外角。
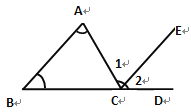
求证:∠ACD=∠A+∠B
证明:过点C作CE∥AB(过直线外一点 )
∴∠B= ( )
∠A= ( )
∵∠ACD=∠1+∠2
∴∠ACD=∠ +∠B(等量代换)
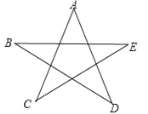
应用:如图是一个五角星,请利用上述结论求
∠A+∠B+∠C+∠D+∠E的值为
【答案】有且只有一条直线与已知直线平行;∠2,(两直线平行,同位角相等 );∠1 ,( 两直线平行,内错角相等 );∠A;180°.
【解析】
过点C作CE∥AB,根据平行线的性质、平角的定义证明;
应用:根据三角形的外角的性质、三角形内角和定理计算即可.
证明:过点C作CE∥AB(过直线外一点 有且只有一条直线与已知直线平行)
∴∠B= ∠2 (两直线平行,同位角相等 )
∠A= ∠1 ( 两直线平行,内错角相等 )
∵∠ACD=∠1+∠2
∴∠ACD=∠A +∠B(等量代换)
应用:如图,对于△BDN,∠MNA=∠B+∠D,

对于△CEM,∠NMA=∠C+∠E,
对于△ANM,∠A+∠MNA+∠NMA=180°,
∴∠A+∠B+∠D+∠C+∠E=180°.
故答案为:有且只有一条直线与已知直线平行;∠2,(两直线平行,同位角相等 );∠1 ,( 两直线平行,内错角相等 );∠A;180°.

练习册系列答案
相关题目