ЬтФПФкШн
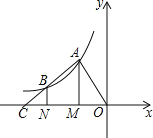
ЁОЬтФПЁПШчЭМЃЌжБЯпl1ЃКyЃНkx+bгыxжсЁЂyжсЗжБ№НЛгкAЃЌBСНЕуЃЌЦфжаЕуBЕФзјБъЮЊЃЈ0ЃЌ6ЃЉЃЌЁЯBAO=30ЁуНЋжБЯпl1бизХyжсе§ЗНЯђЦНвЦвЛЖЮОрРыЕУЕНжБЯпl2НЛyжсгкЕуMЃЌЧвl1гыl2жЎМфЕФОрРыЮЊ3ЃЌЕуCЃЈxЃЌyЃЉЪЧжБЯп11ЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуCзїABЕФДЙЯпCDНЛyжсгкЕуDЃЎ
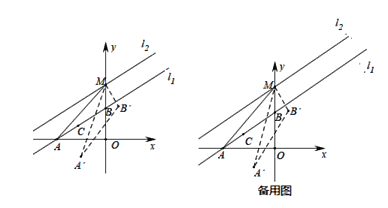
ЃЈ1ЃЉЧѓЕуMЕФзјБъКЭжБЯпl1ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБCдЫЖЏЕНЪВУДЮЛжУЪБЃЌЁїAODЕФУцЛ§ЮЊ21![]() ЃЌЧѓГіДЫЪБЕуCЕФзјБъЃЛ
ЃЌЧѓГіДЫЪБЕуCЕФзјБъЃЛ
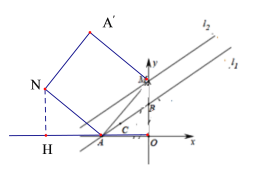
ЃЈ3ЃЉСЌНгAMЃЌНЋЁїABMШЦзХЕуMа§зЊЕУЕНЁїA'B'MЃЌдкЦНУцФкЪЧЗёДцдквЛЕуNЃЎЪЙЫФБпаЮAMA'NЮЊОиаЮЃПШєДцдкЃЌЧѓГіЕуNЕФзјБъЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉM(0ЃЌ6+2![]() )ЃЌжБЯпl1ЕФНтЮіЪНЮЊЃКyЃН
)ЃЌжБЯпl1ЕФНтЮіЪНЮЊЃКyЃН![]() x+6ЃЛЃЈ2ЃЉЕуCЕФзјБъЮЊЃК(-
x+6ЃЛЃЈ2ЃЉЕуCЕФзјБъЮЊЃК(-![]() ЃЌ
ЃЌ![]() )Лђ(
)Лђ(![]() ЃЌ
ЃЌ![]() )ЃЛЃЈ3ЃЉЕуNЕФзјБъЮЊЃК(-6-8
)ЃЛЃЈ3ЃЉЕуNЕФзјБъЮЊЃК(-6-8![]() ЃЌ6
ЃЌ6![]() )Лђ(6-4
)Лђ(6-4![]() ЃЌ-6
ЃЌ-6![]() )ЃЎ
)ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§ЕуBзїBHЁЭl1гкЕуHЃЌгЩl1ЁЮl2ЃЌЕУЁЯBMH=ЁЯOBA=60ЁуЃЌНјЖјЕУBM=2![]() ЃЌМДПЩЕУЕНMЕФзјБъЃЌгЩЬтвтЕУA(-6
ЃЌМДПЩЕУЕНMЕФзјБъЃЌгЩЬтвтЕУA(-6![]() ЃЌ0)ЃЌИљОнД§ЖЈЯЕЪ§ЗЈЃЌМДПЩЕУЕНД№АИЃЛ
ЃЌ0)ЃЌИљОнД§ЖЈЯЕЪ§ЗЈЃЌМДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉСЌНгADЃЌЩшЕуD(0ЃЌm)ЃЌНсКЯЃЌЁїAODЕФУцЛ§ЮЊ21![]() ЃЌЧѓЕУmЕФжЕЮЊЁР7ЃЌЗжСНжжЧщПіЃКЂйЕБD(0ЃЌ-7)ЪБЃЌЂкЕБD(0ЃЌ7)ЪБЃЌЗжБ№ЧѓГіЕуCЕФзјБъМДПЩЃЛ
ЃЌЧѓЕУmЕФжЕЮЊЁР7ЃЌЗжСНжжЧщПіЃКЂйЕБD(0ЃЌ-7)ЪБЃЌЂкЕБD(0ЃЌ7)ЪБЃЌЗжБ№ЧѓГіЕуCЕФзјБъМДПЩЃЛ
ЃЈ3ЃЉгЩЫФБпаЮAMA'NЮЊОиаЮЃЌЧвMA = MA'ЃЌЕУЫФБпаЮAMA'NЮЊе§ЗНаЮЃЌЗжСНжжЧщПіЃКЂйЕБЕуNдкxжсЩЯЗНЪБЃЌЂкЕБЕуNдкxжсЯТЗНЪБЃЌЗжБ№ЧѓГіЕуNЕФзјБъМДПЩЃЎ
ЃЈ1ЃЉЁпЕуBЕФзјБъЮЊ(0ЃЌ6)ЃЌЁЯBAO=30ЁуЃЌЁЯAOB=90ЁуЃЌ
ЁрBO=6ЃЌAO=6![]() ЃЌ
ЃЌ
ЁрA(-6![]() ЃЌ0)ЃЌ
ЃЌ0)ЃЌ
Аб(0ЃЌ6)ЃЌ(-6![]() ЃЌ0)ЃЌДњШыyЃНkx+bЃЌЕУ
ЃЌ0)ЃЌДњШыyЃНkx+bЃЌЕУ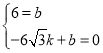 ЃЌНтЕУЃК
ЃЌНтЕУЃК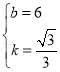 ЃЌ
ЃЌ
ЁржБЯпl1ЕФНтЮіЪНЮЊЃКyЃН![]() x+6ЃЌ
x+6ЃЌ
Й§ЕуBзїBHЁЭl1гкЕуHЃЌШчЭМ1ЃЌ
Ёпl1ЁЮl2ЃЌ
ЁрЁЯBMH=ЁЯOBA=90Ёу-30Ёу=60ЁуЃЌ
ЁрЁЯMBH=30ЁуЃЌ
ЁпBH=3ЃЌ
ЁрBM=3ЁТ![]() ЁС2=2
ЁС2=2![]() ЃЌ
ЃЌ
ЁрM(0ЃЌ6+2![]() )ЃЛ
)ЃЛ
ЃЈ2ЃЉСЌНгADЃЌЩшЕуD(0ЃЌm)ЃЌ
гЩЬтвтЕУЃК![]() OAOD=21
OAOD=21![]() ЃЌ
ЃЌ
Ёр![]() ЁС6
ЁС6![]() ЁС
ЁС![]() =21
=21![]() ЃЌНтЕУЃКm=ЁР7ЃЌ
ЃЌНтЕУЃКm=ЁР7ЃЌ
ЂйЕБD(0ЃЌ-7)ЪБЃЌЙ§ЕуCзїCNЁЭyжсгкЕуNЃЌШчЭМ2ЃЌ
ЁпCDЁЭl2ЃЌ
ЁрЁЯCDB=90Ёу-ЁЯABO=90Ёу-60Ёу=30ЁуЃЌ
ЁпBD=OB+OD=6+7=13ЃЌ
ЁрCD=13ЁТ2ЁС![]() =
=![]() ЃЌCN=
ЃЌCN=![]() CD=
CD=![]() ЃЌDN=
ЃЌDN=![]() CN=
CN=![]() ЃЌ
ЃЌ
ЁрON=![]() -7=
-7=![]() ЃЌ
ЃЌ
ЁрC(-![]() ЃЌ
ЃЌ![]() )ЃЛ
)ЃЛ
ЂкЕБD(0ЃЌ7)ЪБЃЌЭЌРэПЩЕУЃКC(![]() ЃЌ
ЃЌ![]() )ЃЌ
)ЃЌ
злЩЯЫљЪіЃКЕуCЕФзјБъЮЊЃК(-![]() ЃЌ
ЃЌ![]() )Лђ(
)Лђ(![]() ЃЌ
ЃЌ![]() )ЃЛ
)ЃЛ
ЃЈ3ЃЉДцдкЃЌРэгЩШчЯТЃК
ЁпЫФБпаЮAMA'NЮЊОиаЮЃЌЧвMA = MA'ЃЌ
ЁрЫФБпаЮAMA'NЮЊе§ЗНаЮЃЌ
ЁрAN=AMЃЌ
ЂйЕБЕуNдкxжсЩЯЗНЪБЃЌЙ§ЕуNзїNHЁЭxжсгкЕуNЃЌШчЭМ3ЃЌ
ЁпЁЯAHN=ЁЯMAN=ЁЯAOM=90ЁуЃЌ
ЁрЁЯHAN+ЁЯOAM=ЁЯOAM+ЁЯAMO=90ЁуЃЌ
ЁрЁЯHAN=ЁЯAMOЃЌ
ЁрAHNMOAЃЈAASЃЉЃЌ
ЁрNH=OA=6![]() ЃЌAH=OM=6+2
ЃЌAH=OM=6+2![]() ЃЌ
ЃЌ
ЁрOH=AH+OA=6+8![]() ЃЌ
ЃЌ
ЁрN(-6-8![]() ЃЌ6
ЃЌ6![]() )ЃЌ
)ЃЌ
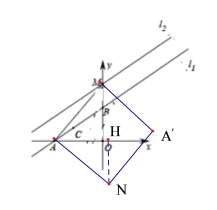
ЂкЕБЕуNдкxжсЯТЗНЪБЃЌЙ§ЕуNзїNHЁЭxжсгкЕуNЃЌШчЭМ4ЃЌ
ЭЌРэПЩЕУЃКAHNMOAЃЈAASЃЉЃЌ
ЁрNH=OA=6![]() ЃЌAH=OM=6+2
ЃЌAH=OM=6+2![]() ЃЌ
ЃЌ
ЁрOH=AH-OA=6-4![]() ЃЌ
ЃЌ
ЁрN(6-4![]() ЃЌ-6
ЃЌ-6![]() )ЃЌ
)ЃЌ
злЩЯЫљЪіЃКЕуNЕФзјБъЮЊЃК(-6-8![]() ЃЌ6
ЃЌ6![]() )Лђ(6-4
)Лђ(6-4![]() ЃЌ-6
ЃЌ-6![]() )ЃЎ
)ЃЎ
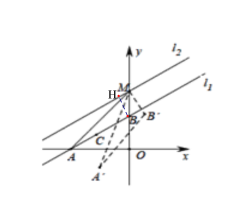
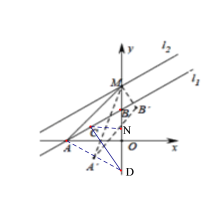
ЭМ1 ЭМ2
ЭМ3 ЭМ4