题目内容
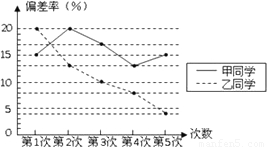
(2008•江西)为了了解甲、乙两同学对“字的个数”的估计能力,现场对他们进行了5次测试,测试方法是:拿出一张报纸,随意用笔画一个圈,让他们看了一眼后迅速说出圈内有多少个汉字,但不同的是:甲同学每次估计完字数后不告诉他圈内的实际字数,乙同学每次估计完字数后告诉他圈内的实际字数.根据甲、乙两同学5次估计情况可绘制统计图如下:(1)结合上图提供的信息,就甲、乙两同学分别写出两条不同类型的正确结论;
(2)若对甲、乙两同学进行第6次测试,当所圈出的实际字数为100个时,请你用统计知识分别预测他们估计字数的偏差率,并根据预测的偏差率,推算出他们估计的字数所在的范围.

【答案】分析:(1)此题要分情况而论,所以学生一定要培养严密的思维;
(2)分三种情况去考虑:①从平均偏差率预测;②从偏差率的中位数预测;③从偏差率的变化情况预测.
解答:解:(1)可从不同角度分析.例如:
①甲同学的平均偏差率是16%,乙同学的平均偏差率是11%;
②甲同学的偏差率的极差是7%,乙同学的偏差率的极差是16%;
③甲同学的偏差率最小值是13%,乙同学的偏差率最小值是4%;
④甲、乙两同学的偏差率最大值都是20%;
⑤甲同学对字数的估计能力没有明显的提高,乙同学对字数的估计能力有明显提高.(4分)
(2)可从不同角度分析.例如:
①从平均偏差率预测:
甲同学的平均偏差率是16%,估计的字数所在范围是84~116;(6分)
乙同学的平均偏差率是11%,估计的字数所在范围是89~111;(8分)
②从偏差率的中位数预测:
甲同学偏差率的中位数是15%,估计的字数所在范围是85~115;(6分)
乙同学偏差率的中位数是10%,估计的字数所在范围是90~110;(8分)
③从偏差率的变化情况预测:
甲同学的偏差率没有明显的趋势特征,可有多种预测方法,如偏差率的最大值与最小值的平均值是16.5%,估计的字数所在范围是84~116或83~117.(6分)
乙同学的偏差率是0%~4%,估计的字数所在的范围是96~104或其它.(8分)
点评:本题是一道统计题,它结合学生熟悉的现实背景“估计字数字”,再增加一个新定义--“偏差率”,构成了一道立意非常新颖的统计开放题.主要考查学生利用折线统计图所反映出来的统计量进行分析和预测推断的能力,这正是统计内容中需要考查的核心知识.从试题的形式上看,赋予了学生很大的答题自由度,有利于学生展示自已对统计图、统计量等知识的认识.
(2)分三种情况去考虑:①从平均偏差率预测;②从偏差率的中位数预测;③从偏差率的变化情况预测.
解答:解:(1)可从不同角度分析.例如:
①甲同学的平均偏差率是16%,乙同学的平均偏差率是11%;
②甲同学的偏差率的极差是7%,乙同学的偏差率的极差是16%;
③甲同学的偏差率最小值是13%,乙同学的偏差率最小值是4%;
④甲、乙两同学的偏差率最大值都是20%;
⑤甲同学对字数的估计能力没有明显的提高,乙同学对字数的估计能力有明显提高.(4分)
(2)可从不同角度分析.例如:
①从平均偏差率预测:
甲同学的平均偏差率是16%,估计的字数所在范围是84~116;(6分)
乙同学的平均偏差率是11%,估计的字数所在范围是89~111;(8分)
②从偏差率的中位数预测:
甲同学偏差率的中位数是15%,估计的字数所在范围是85~115;(6分)
乙同学偏差率的中位数是10%,估计的字数所在范围是90~110;(8分)
③从偏差率的变化情况预测:
甲同学的偏差率没有明显的趋势特征,可有多种预测方法,如偏差率的最大值与最小值的平均值是16.5%,估计的字数所在范围是84~116或83~117.(6分)
乙同学的偏差率是0%~4%,估计的字数所在的范围是96~104或其它.(8分)
点评:本题是一道统计题,它结合学生熟悉的现实背景“估计字数字”,再增加一个新定义--“偏差率”,构成了一道立意非常新颖的统计开放题.主要考查学生利用折线统计图所反映出来的统计量进行分析和预测推断的能力,这正是统计内容中需要考查的核心知识.从试题的形式上看,赋予了学生很大的答题自由度,有利于学生展示自已对统计图、统计量等知识的认识.

练习册系列答案
相关题目
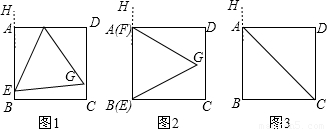
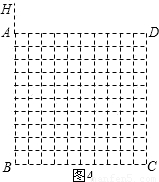
(2008•江西)如图1,正方形ABCD和正三角形EFG的边长都为1,点E,F分别在线段AB,AD上滑动,设点G到CD的距离为x,到BC的距离为y,记∠HEF为α(当点E,F分别与B,A重合时,记α=0°).
(1)当α=0°时(如图2所示),求x,y的值(结果保留根号);
(2)当α为何值时,点G落在对角形AC上?请说出你的理由,并求出此时x,y的值(结果保留根号);
(3)请你补充完成下表(精确到0.01):
(4)若将“点E,F分别在线段AB,AD上滑动”改为“点E,F分别在正方形ABCD边上滑动”.当滑动一周时,请使用(3)的结果,在图4中描出部分点后,勾画出点G运动所形成的大致图形.
(参考数据: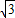 ≈1.732,sin15°=
≈1.732,sin15°=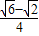 ≈0.259,sin75°=
≈0.259,sin75°=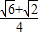 ≈0.966)
≈0.966)
(1)当α=0°时(如图2所示),求x,y的值(结果保留根号);
(2)当α为何值时,点G落在对角形AC上?请说出你的理由,并求出此时x,y的值(结果保留根号);
(3)请你补充完成下表(精确到0.01):
| α | 0° | 15° | 30° | 45° | 60° | 75° | 90° |
| x | 0.03 | 0.29 | |||||
| y | 0.29 | 0.13 | 0.03 |
(参考数据:
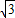 ≈1.732,sin15°=
≈1.732,sin15°=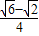 ≈0.259,sin75°=
≈0.259,sin75°=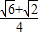 ≈0.966)
≈0.966)