题目内容
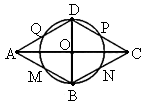
求证：菱形各边中点在以对角线的交点为圆心的同一个圆上．分析：如图，菱形ABCD的对角线AC和BD相交于点O，菱形ABCD各边中点分别为M、N、P、Q，根据菱形的性质得到AC⊥BD，垂足为O，且AB=BC=CD=DA，再根据直角三角形斜边上的中线等于斜边的一半得到OM=ON=OP=OQ=
AB，得到M、N、P、Q四点在以O为圆心OM为半径的圆上．
| 1 |
| 2 |
解答：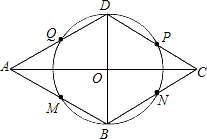
已知：如图，菱形ABCD的对角线AC和BD相交于点O．
求证：菱形ABCD各边中点M、N、P、Q在以O为圆心的同一个圆上．
证明：∵四边形ABCD是菱形，
∴AC⊥BD，垂足为O，且AB=BC=CD=DA，
而M、N、P、Q分别是边AB、BC、CD、DA的中点，
∴OM=ON=OP=OQ=
AB，
∴M、N、P、Q四点在以O为圆心OM为半径的圆上．
所以菱形各边中点在以对角线的交点为圆心的同一个圆上．
已知：如图，菱形ABCD的对角线AC和BD相交于点O．求证：菱形ABCD各边中点M、N、P、Q在以O为圆心的同一个圆上．
证明：∵四边形ABCD是菱形，
∴AC⊥BD，垂足为O，且AB=BC=CD=DA，
而M、N、P、Q分别是边AB、BC、CD、DA的中点，
∴OM=ON=OP=OQ=
| 1 |
| 2 |
∴M、N、P、Q四点在以O为圆心OM为半径的圆上．
所以菱形各边中点在以对角线的交点为圆心的同一个圆上．
点评：本题考查了四点共圆的判定方法．也考查了菱形的性质以及直角三角形斜边上的中线等于斜边的一半．
练习册系列答案
相关题目
