题目内容
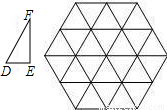
 如图,△DEF的边长分别为1,
如图,△DEF的边长分别为1, ,2,正六边形网格是由24个边长为2的正三角形组成,以这些正三角形的顶点为顶点画△ABC,使得△ABC∽△DEF.如果相似比
,2,正六边形网格是由24个边长为2的正三角形组成,以这些正三角形的顶点为顶点画△ABC,使得△ABC∽△DEF.如果相似比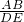 =k,那么k的不同的值共有
=k,那么k的不同的值共有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:根据题意可得:在正六边形网格找与△DEF相似的三角形;即找三边的比值为1: :2的直角三角形;分析图形可得:共三种情况,相似比分别为:2,2
:2的直角三角形;分析图形可得:共三种情况,相似比分别为:2,2 ,4;
,4;
解答:∵△DEF的边长分别为1, ,2
,2
∴△DEF为直角三角形,∠F=30°,∠D=60°
根据等边三角形的三线合一,可作三边比为1:( +
+ ):2的三角形
):2的三角形
∴相似比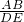 =k,k可取2,2
=k,k可取2,2 ,4.
,4.
故选C.
点评:本题主要考查了相似三角形的判定.
分析:根据题意可得:在正六边形网格找与△DEF相似的三角形;即找三边的比值为1:
 :2的直角三角形;分析图形可得:共三种情况,相似比分别为:2,2
:2的直角三角形;分析图形可得:共三种情况,相似比分别为:2,2 ,4;
,4;解答:∵△DEF的边长分别为1,
 ,2
,2∴△DEF为直角三角形,∠F=30°,∠D=60°
根据等边三角形的三线合一,可作三边比为1:(
 +
+ ):2的三角形
):2的三角形∴相似比
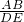 =k,k可取2,2
=k,k可取2,2 ,4.
,4.故选C.
点评:本题主要考查了相似三角形的判定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
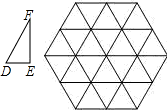
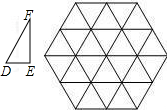 如图,△DEF的边长分别为1,
如图,△DEF的边长分别为1,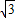 ,2,正六边形网格是由24个边长为2的正三角形组成,以这些正三角形的顶点为顶点画△ABC,使得△ABC∽△DEF.如果相似比
,2,正六边形网格是由24个边长为2的正三角形组成,以这些正三角形的顶点为顶点画△ABC,使得△ABC∽△DEF.如果相似比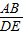 =k,那么k的不同的值共有( )
=k,那么k的不同的值共有( )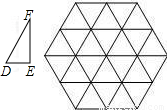
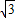 ,2,正六边形网格是由24个边长为2的正三角形组成,以这些正三角形的顶点为顶点画△ABC,使得△ABC∽△DEF.如果相似比
,2,正六边形网格是由24个边长为2的正三角形组成,以这些正三角形的顶点为顶点画△ABC,使得△ABC∽△DEF.如果相似比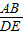 =k,那么k的不同的值共有( )
=k,那么k的不同的值共有( )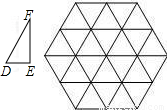
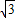 ,2,正六边形网格是由24个边长为2的正三角形组成,以这些正三角形的顶点为顶点画△ABC,使得△ABC∽△DEF.如果相似比
,2,正六边形网格是由24个边长为2的正三角形组成,以这些正三角形的顶点为顶点画△ABC,使得△ABC∽△DEF.如果相似比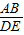 =k,那么k的不同的值共有( )
=k,那么k的不同的值共有( )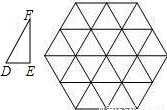
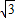 ,2,正六边形网格是由24个边长为2的正三角形组成,以这些正三角形的顶点为顶点画△ABC,使得△ABC∽△DEF.如果相似比
,2,正六边形网格是由24个边长为2的正三角形组成,以这些正三角形的顶点为顶点画△ABC,使得△ABC∽△DEF.如果相似比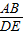 =k,那么k的不同的值共有( )
=k,那么k的不同的值共有( )