Question

如图，l1、l2、l3、l4是同一平面内的四条平行直线，且每相邻的两条平行直线间的距离都为h，正方形ABCD的四个顶点分别在这四条直线上，且正方形ABCD的面积是25． (1)证明△ABE、△FBE、△EDF、△CDF的面积都相等； (2)求h的值．

Answer 1

答案：
解析：

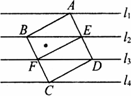
(1)证明：∵l1∥l2∥l3∥l4，且四边形ABCD是正方形， 　　∴BE∥FD，BF∥ED， 　　∴四边形EBFD为平行四边形， 　　∴BE＝FD． 　　又∵l1、l2、l3和l4，之间的距离都为h， 　　∴，，， 　　∴S△ABE＝S△FBE＝S△EDF＝S△CDF． 　　(2)解：过A点作AH⊥BE于H点． 　　∵S△ABE＝S△FBE＝S△EDF＝S△CDF， 　　正方形ABCD的面积是25， 　　，且AB＝AD＝5． 　　又∵l1∥l2∥l3∥l4， 　　∴E、F分别是边AD与BC的中点， 　　． 　　∴在Rt△ABE中， 　　． 　　∵AB·AE＝BE·AH， 　　∴． 　　即h的值为．