题目内容
【题目】如图，△ABC是一张三角形的纸片，⊙O是它的内切圆，点D是其中的一个切点，已知AD=10cm ， 小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形（△AMN），则剪下的△AMN的周长为（ ）
A.20cm
B.15cm
C.10cm
D.随直线MN的变化而变化
【答案】A
【解析】 如图：
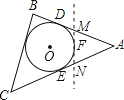
∵△ABC是一张三角形的纸片，⊙O是它的内切圆，点D是其中的一个切点，AD=10cm，
∴设E、F分别是⊙O的切点，
故DM=MF，FN=EN，AD=AE，
∴AM+AN+MN=AD+AE=10+10=20（cm）．
所以答案是：A．
【考点精析】关于本题考查的切线长定理，需要了解从圆外一点引圆的两条切线，它们的切线长相等圆心和这一点的连线平分两条切线的夹角才能得出正确答案．
练习册系列答案
阅读快车系列答案
相关题目
