题目内容
10、如图，已知AD=AE，BE=CD，∠1=∠2=110°，∠BAC=80°，则∠CAE的度数是（ ）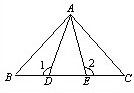
分析：由题意知，△ABD和△ABC是等腰三角形，可求得顶角∠DAE的度数，及∠BAD=∠EAC，进而求得∠CAE的度数．
解答：解：∵AD=AE，BE=CD，
∴△ABD和△ABC是等腰三角形．
∴∠B=∠C，∠ADE=∠AED．
∵∠1=∠2=110°，
∴∠ADE=∠AED=70°．
∴∠DAE=180°-2×70°=40°．
∵∠1=∠2=110°，∠B=∠C，
∴∠BAD=∠EAC．
∵∠BAC=80°．
∴∠BAD=∠EAC=（∠BAC-∠DAE）÷2=20°．
故选A．
∴△ABD和△ABC是等腰三角形．
∴∠B=∠C，∠ADE=∠AED．
∵∠1=∠2=110°，
∴∠ADE=∠AED=70°．
∴∠DAE=180°-2×70°=40°．
∵∠1=∠2=110°，∠B=∠C，
∴∠BAD=∠EAC．
∵∠BAC=80°．
∴∠BAD=∠EAC=（∠BAC-∠DAE）÷2=20°．
故选A．
点评：本题利用了等边对等角，三角形内角和定理求解．
练习册系列答案
相关题目
18、如图，已知AD=AE，AB=AC．
如图，已知AD=AE，要使△ADC≌△AEB，还需添加一个条件，那么这个条件可以是
如图，已知AD=AE，添加下列条件仍无法证明△ABE≌△ACD的是（ ）
如图，已知AD=AE，∠1=∠2，BD=CE，那么有△ABD≌