题目内容
已知点M,N的坐标分别为(0,1),(0,-1),点P是抛物线y=| 1 |
| 4 |
(1)求证:以点P为圆心,PM为半径的圆与直线y=-1的相切;
(2)设直线PM与抛物线y=
| 1 |
| 4 |
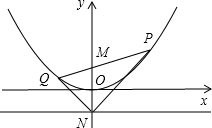
分析:(1)可先根据抛物线的解析式设出P点的坐标,那么可得出PM的长的表达式,P点到y=-1的长就是P点的纵坐标与-1的差的绝对值,那么可判断得出的表示PM和P到y=-1的距离的两个式子是否相等,如果相等,则y=-1是圆P的切线.
(2)可通过构建相似三角形来求解,过Q,P作QR⊥直线y=-1,PH⊥直线y=-1,垂足为R,H,那么QR∥MN∥PH,根据平行线分线段成比例定理可得出QM:MP=RN:NH.(1)中已得出了PM=PH,那么同理可得出QM=QR,那么比例关系式可写成QR:PH=RN:NH,而这两组对应成比例的线段的夹角又都是直角,因此可求出∠QNR=∠PNH,根据等角的余角相等,可得出∠QNM=∠PNM.
(2)可通过构建相似三角形来求解,过Q,P作QR⊥直线y=-1,PH⊥直线y=-1,垂足为R,H,那么QR∥MN∥PH,根据平行线分线段成比例定理可得出QM:MP=RN:NH.(1)中已得出了PM=PH,那么同理可得出QM=QR,那么比例关系式可写成QR:PH=RN:NH,而这两组对应成比例的线段的夹角又都是直角,因此可求出∠QNR=∠PNH,根据等角的余角相等,可得出∠QNM=∠PNM.
解答:解:(1)设点P的坐标为(x0,
x20),则
PM=
=
x20+1;
又因为点P到直线y=-1的距离为,
x20-(-1)=
x20+1
所以,以点P为圆心,PM为半径的圆与直线y=-1相切.
(2)如图,分别过点P,Q作直线y=-1的垂线,垂足分别为H,R.
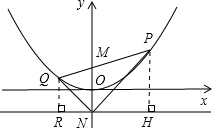
由(1)知,PH=PM,同理可得,QM=QR.
因为PH,MN,QR都垂直于直线y=-1,
所以,PH∥MN∥QR,
于是
=
,
所以
=
,
因此,Rt△PHN∽Rt△QRN.
于是∠HNP=∠RNQ,从而∠PNM=∠QNM.
| 1 |
| 4 |
PM=
|
| 1 |
| 4 |
又因为点P到直线y=-1的距离为,
| 1 |
| 4 |
| 1 |
| 4 |
所以,以点P为圆心,PM为半径的圆与直线y=-1相切.
(2)如图,分别过点P,Q作直线y=-1的垂线,垂足分别为H,R.

由(1)知,PH=PM,同理可得,QM=QR.
因为PH,MN,QR都垂直于直线y=-1,
所以,PH∥MN∥QR,
于是
| QM |
| RN |
| MP |
| NH |
所以
| QR |
| RN |
| PH |
| HN |
因此,Rt△PHN∽Rt△QRN.
于是∠HNP=∠RNQ,从而∠PNM=∠QNM.
点评:本题主要考查了相似三角形的性质,平行的性质以及二次函数和一次函数的综合应用.
(2)中通过构建相似三角形来求角相等是解题的关键.
(2)中通过构建相似三角形来求角相等是解题的关键.

练习册系列答案
相关题目
 里a>0,且a为常数.直线EF和抛物线的对称轴交于点B,和直线x=2交于点D.
里a>0,且a为常数.直线EF和抛物线的对称轴交于点B,和直线x=2交于点D. 如图,已知点A、B的坐标分别是(0,0)(4,0),将△ABC绕A点按逆时针方向旋转90°后得到△A′B′C′
如图,已知点A、B的坐标分别是(0,0)(4,0),将△ABC绕A点按逆时针方向旋转90°后得到△A′B′C′
