��Ŀ����
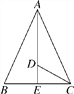
����Ŀ����ͼ����ABC�Ķ���A��B��C����С�����εĶ����ϣ����ABC�����������νи�������Σ����ڷ���ֽ�ϰ�����Ҫ��������Σ�
��1������ABC������ƽ��4����λ��������ƽ��2����λ�õ���A1B1C1��(A1��B1��C1�Ķ�Ӧ��ֱ�ΪA��B��C)
��2���߶�AC��A1C1�Ĺ�ϵ ��
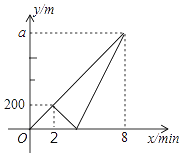
��3����AB���ϵ�����CD����CE��������������ֱ��ͼ��
��4������CC1�����BCC1�� �㣮

���𰸡���1����������2��ƽ������ȣ�3����������4��45��
����������������1����A��B��C��ƽ�������ҳ����ǵĶ�Ӧ����˳�����������õ�ƽ�ƺ��ͼ����
��2����ƽ�Ƶ����ʼ��ɵõ�������
��3���ó߹���ͼ������
��4�����ù��ɶ������涨���ó���BCC1�ǵ���ֱ�������ν��������BCC1��
�������1����ͼ��ʾ��
��2����ƽ�Ƶ����ʿɵ���AC��A1C1ƽ���������
��3����ͼ��
��4����BC=![]() =
=![]() ��BC1=
��BC1=![]() =
=![]() ��CC1=
��CC1=![]() =2
=2![]() ��BC2+BC
��BC2+BC![]() =C1C2�����BCC1�ǵ���ֱ�������������BCC1=45�㣮
=C1C2�����BCC1�ǵ���ֱ�������������BCC1=45�㣮
�ʴ�Ϊ��45��


����Ŀ��ij�̵깺��һ����Ʒ��ÿ����Ʒ����30Ԫ�������з���������Ʒÿ���������y��������ÿ�����ۼ�x��Ԫ���Ĺ�ϵ�������£�
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
��1����֪y��x����һ�κ�����ϵ�������ϱ������y��x֮��Ĺ�ϵʽ����д���Ա���x��ȡֵ��Χ����
��2������̵�����������Ʒ��ÿ��Ҫ���150Ԫ������ôÿ����Ʒ�����ۼ�Ӧ��Ϊ����Ԫ��
��3������̵�ÿ������������Ʒ��������Ϊw��Ԫ�������w��x֮��Ĺ�ϵʽ�������ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ�������
����Ŀ��Ԫ���ڼ䣬Ϊ����������ذ��յ�������Ҫ��ij�����̳��ƻ���170000Ԫ����һ���ҵ磬��������Ľ��ۺ��ۼ������
��� | �ʵ� | ���� | ϴ�»� |
���ۣ�Ԫ/̨�� | 2000 | 1600 | 1000 |
�ۼۣ�Ԫ/̨�� | 2300 | 1800 | 1100 |
���������ʽ������ķ�Χ�ڣ������������ҵ繲100̨�����вʵ�̨���DZ���̨����2��������̳��������x̨��
��1���ú�x�Ĵ���ʽ��ʾϴ�»���̨����
��2���̳�������Թ���������̨��
��3������������̨ʱ����ʹ�̳������������ҵ���õ���������������Ϊ����Ԫ��