Question

已知

AB

和

CD

是同圆中的两条弧，且

CD

=2

AB

，那么弦AB与

1

2

CD的大小关系是（　　）

• A．AB＜

  1

  2

  CD
• B．AB＞

  1

  2

  CD
• C．AB=

  1

  2

  CD
• D．无法确定

Answer 1

分析：取弧CD的中点E，可以得出CE=DE=AB，由三角形的三边关系：两边之和大于第三边，就可以得2AB＞CD，从而得出结论．

解答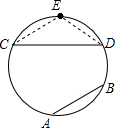：解：如图，作弧CD的中点E，连接CE、DE，
∴

CD

=2

CE

=2

DE

，
∴CE=DE，
∵

CD

=2

AB

，
∴

CE

=

DE

=

AB

，
∴CE=DE=AB，
∴CE+DE=2AB．
∵CE+DE＞CD，
∴2AB＞CD，
∴AB＞

1

2

CD．
故选B．

点评：本题考查了圆心角、弧、弦的关系，三角形三边关系的运用，线段的转化等多个知识点，难度适中．