题目内容
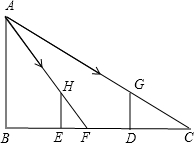如图，小明站在竖立的电线杆AB前D处时的影子长为3m，他向电线杆走了4m到达E处时的影子长为1m．若小明的身高为1.8m．（1）求电线杆的长；
（2）找出△ABF的位似图形，并指出位似中心．
分析：（1）根据在E处时△ABF和△HEF相似，在D处时△ABC和△GDC相似，利用相似三角形对应边成比例列出比例式，再根据小明的身高HE与GD相等，然后两比例式联立求解即可；
（2）根据位似变换的定义即可找出位似图形与位似中心．
（2）根据位似变换的定义即可找出位似图形与位似中心．
解答：解：（1）在△ABF和△HEF中．
∠B=∠HEF=90°，∠BFA=∠EFH，
则△ABF∽△HEF，
∴
=
，
即
=
①，（3分）
在△ABC和△GDC中，∠B=∠GDC=90°，∠C=∠C，
则△ABC∽△GDC，
∴
=
，
即
=
②，（6分）
而HE=GD③，
由①、②、③可得BE+1=
，
解得BE=2．
把BE=2代入①中，
得AB=（2+1）HE=1.8×3=5.4（m）；（8分）
（2）△ABF的位似图形是△HEF．位似中心是点F．（10分）
说明：以上各题若用其它做法可参照此标准评分．
∠B=∠HEF=90°，∠BFA=∠EFH，
则△ABF∽△HEF，
∴
| AB |
| HE |
| BF |
| EF |
即
| AB |
| HE |
| BE+1 |
| 1 |
在△ABC和△GDC中，∠B=∠GDC=90°，∠C=∠C，
则△ABC∽△GDC，
∴
| AB |
| GD |
| BC |
| DC |
即
| AB |
| GD |
| BE+4+3 |
| 3 |
而HE=GD③，
由①、②、③可得BE+1=
| BE+7 |
| 3 |
解得BE=2．
把BE=2代入①中，
得AB=（2+1）HE=1.8×3=5.4（m）；（8分）
（2）△ABF的位似图形是△HEF．位似中心是点F．（10分）
说明：以上各题若用其它做法可参照此标准评分．
点评：本题主要考查了相似三角形的应用，根据相似三角形对应边成比例列出比例式是解题的关键，本题中线段HE与GD是小明的身高，相等是联系两比例式的纽带．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
如图，小明站在竖立的电线杆AB前D处时的影子长为3m，他向电线杆走了4m到达E处时的影子长为1m．若小明的身高为1.8m．