题目内容
【题目】如图,在⊙O中,M是弦AB的中点,过点B作⊙O的切线,与OM延长线交于点C.

(1)求证:∠A=∠C;
(2)若OA=5,AB=8,求线段OC的长.
【答案】(1)见解析(2)![]()
【解析】
(1)连接OB,由OA=OB,可知∠A=∠OBM,又M是AB中点,利用等腰三角形三线合一定理可知OC⊥AB,即可得∠C+∠CBM=90°,而BC是切线可得∠OBM+∠CBM=90°,即∠A+∠CBM=90°,利用等角的余角相等可得∠A=∠C;
(2)由(1)得∠C=∠OBM,∠OBC=∠OMB=90°,易证△OMB∽△OBC,即可得OB:OC=OM:OB,而BM=![]() AB=4,根据勾股定理可求OM,进而即可求出OC的长.
AB=4,根据勾股定理可求OM,进而即可求出OC的长.
(1)证明:连接OB,
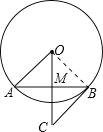
∵BC是切线,
∴∠OBC=90°,
∴∠OBM+∠CBM=90°,
∵OA=OB,
∴∠A=∠OBM,
∵M是AB的中点,
∴OM⊥AB.
∴∠C+∠CBM=90°,
∴∠C=∠OBM,
∴∠A=∠C;
(2)∵∠C=∠OBM,∠OBC=∠OMB=90°,
∴△OMB∽△OBC,
∴![]() =
=![]() ,
,
又∵BM=![]() AB=4,
AB=4,
∴OM=52-42=3,
∴OC=![]() =
=![]() .
.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】某商场销售A、B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
教学设备 | A | B |
进价(万元/套) | 3 | 2.4 |
售价(万元/套) | 3.3 | 2.8 |
该商场计划购进两种教学设备若干套,共需132万元,全部销售后可获毛利润18万元.
(1)该商场计划购进A、B两种品牌的教学设备各多少套?
(2)通过市场调查,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍.若用于购进这两种教学设备的总资金不超过138万元,则A种设备购进数量最多减少多少套?