题目内容
如图，把△ABC纸片沿DE折叠，使点A落在四边形BCDE的内部，若∠A=40°，则∠1+∠2=________°．
80
分析：根据平角定义和折叠的性质，得∠1+∠2=360°-2（∠3+∠4），再利用三角形的内角和定理进行转换，得∠1+∠2=360°-2（180°-∠A）=2∠A．
解答：根据平角的定义和折叠的性质，得
∠1+∠2=360°-2（∠3+∠4）．
又∠3+∠4=180°-∠A，
∴∠1+∠2=360°-2（180°-∠A）=2∠A=80°．
点评：此题综合运用了平角的定义、折叠的性质和三角形的内角和定理．
分析：根据平角定义和折叠的性质，得∠1+∠2=360°-2（∠3+∠4），再利用三角形的内角和定理进行转换，得∠1+∠2=360°-2（180°-∠A）=2∠A．
解答：根据平角的定义和折叠的性质，得
∠1+∠2=360°-2（∠3+∠4）．
又∠3+∠4=180°-∠A，
∴∠1+∠2=360°-2（180°-∠A）=2∠A=80°．
点评：此题综合运用了平角的定义、折叠的性质和三角形的内角和定理．
练习册系列答案
相关题目
如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，
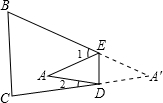
20、如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE的外部时，∠A与∠1、∠2之间存在一种始终保持不变的数量关系，这个数量关系是
如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，